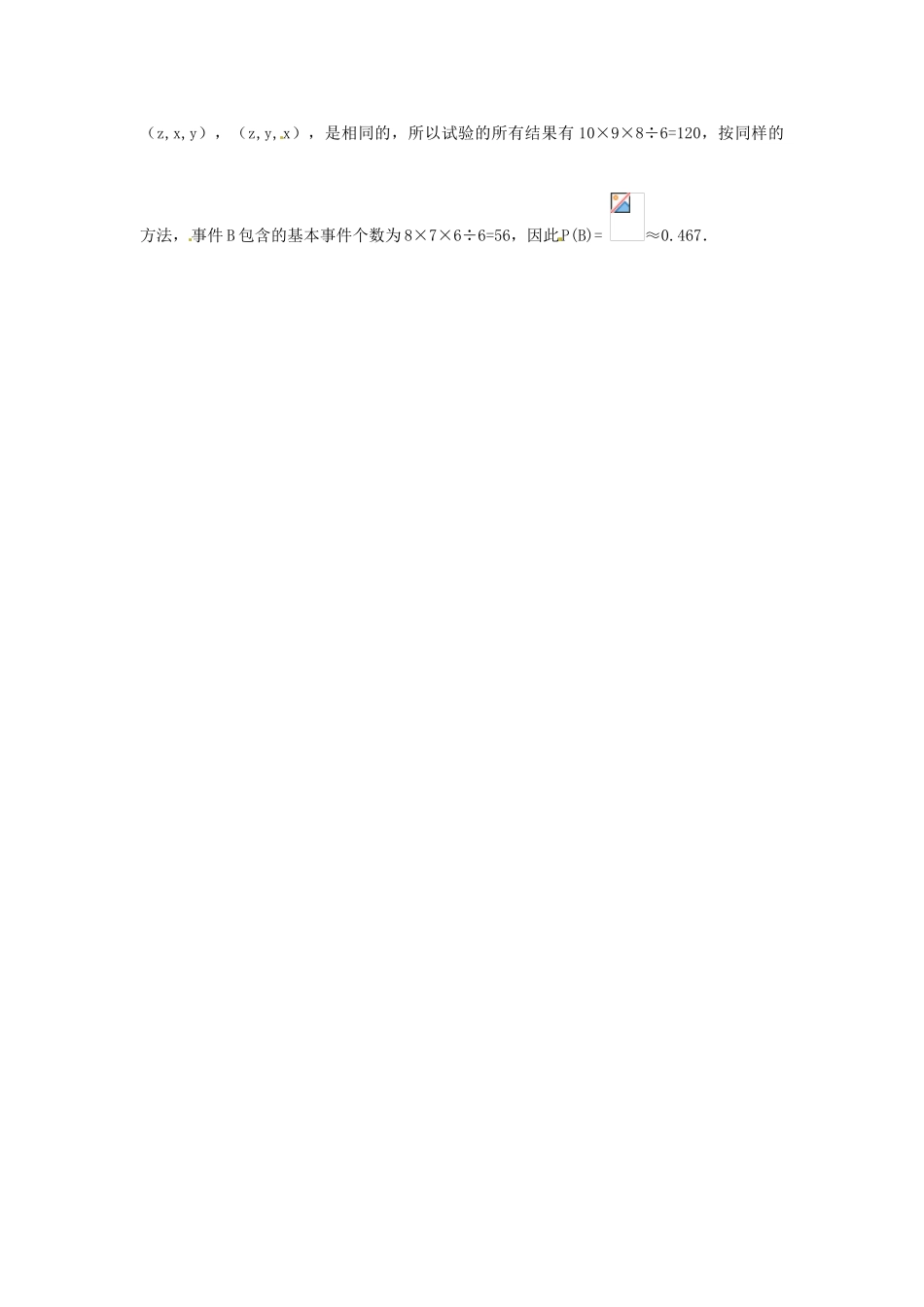
古典概型学习过程知识点一:基本事件的定义试验结果是有限个,且每个事件都是随机事件的事件称为基本事件。知识点二:基本事件的特点:(1)任何两个基本事件是互斥的;(2)任何事件(除不可能事件)都可以表示成基本事件的和。知识点三:古典概型(1)试验中所有可能出现的基本事件只有有限个;(2)每个基本事件出现的可能性相等。我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。知识点四:古典概型的概率公式P(A)=学习结论:(1)古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等(2)写基本事件时,为了不重不漏,我们需按一定顺序把结果一一列举出来。典型例题:例 1.掷一颗骰子,观察掷出的点数,求掷得奇数点的概率。答案:0.5分析:掷骰子有 6 个基本事件,具有有限性和等可能性,因此是古典概型。解析:这个试验的基本事件共有 6 个,即(出现 1 点)、(出现 2 点)……、(出现 6点)所以基本事件数 n=6,事件 A=(掷得奇数点)=(出现 1 点,出现3 点,出现 5 点),其包含的基本事件数 m=3所以,P(A)====0.5例 2 从含有两件正品 a1,a2 和一件次品 b1 的三 件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率。答案:解析:每次取出一 个,取后不放回地连续取两次,其一切可 能的结果组成的基本事件有 6个,即(a1,a2)和,(a1,b1),(a2,a 1),(a2,b1),(b1,a1),(b1,a2)。其中小括号内左边的字母表示第 1 次取出的产品,右边的字母表示第 2 次取出的产用 A 表示“取出的两种中,恰好有一件次品”这一事件,则A=[((a1,b1),(a2,b1),(b1,a1),(b1,a2)]事件 A 由 4 个基本事件组成,因而,P(A)==例 3 现有一批产品共有 10 件,其中 8 件为正品,2 件为次品:(1)如果从中取出一件,然后放回,再取一件,求连续 3 次取出的都是正品的概率;(2)如果从中一次取 3 件,求 3 件都是正品的概率.答案:(1)0.512 (2)0.467分析:(1)为返回抽样;(2)为不返回抽样.解析:(1)有放回地抽取 3 次,按抽取顺序(x,y,z)记录结果,则 x,y,z 都有 10 种可能,所以试验结果有 10×10×10=103 种;设事件 A 为“连续 3 次都取正品”,则包含的基本 事件共有 8×8×8=83 种,因此,P(A)= =0.512.(2)解法 1:可...