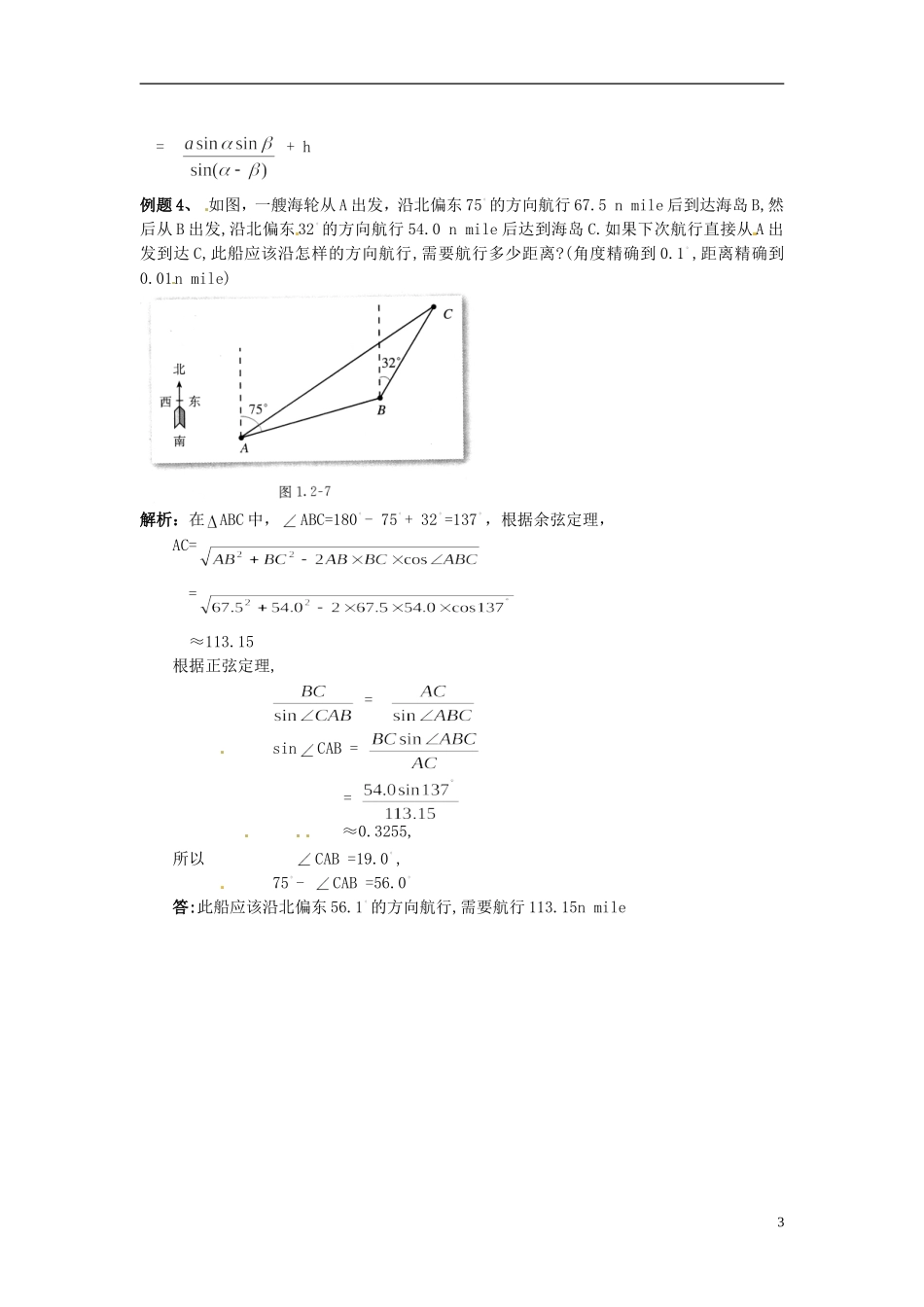
应用举例学习过程知识点 1:运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语知识点 2 运用正弦 定理、余弦定理等知识和方法解决一些有关底部不可到达的物体高度测量的问题知识点 3 运用正弦定理、余弦定理等知识和方法解决一些有关计算角度的实际问题学习结论:正确利用正弦定理、余弦定理解决实际问题典型例题例题 1、如图,设 A、B两点在河的两岸,要测量两点之间的距离,测量者在 A 的同侧,在所在的河岸边选定一点 C,测出 AC 的距离是 55m,,。求 A、B 两点的距离(精确到 0.1m)解析:根据正弦定理,得 ≈ 65.7(m)答:A、B 两点间的距离为 65.7 米例题 2、如图,A、B 两点都在河的对岸(不可到达),设计一种测量 A、B 两点间距离的方法。1解析:测量者可以在河岸边选定两点 C、D,测得 CD=a,并且在 C、D 两点分别测得,,,,在ADC 和BDC 中,应用正弦定理AC = = BC = = 计算出 AC 和 BC 后,再在ABC 中,应用余弦定理计算出 AB 两点间的距离 AB = cos222BCACBCAC例题 3、 AB 是底部 B 不可到达的一个建筑物,A 为建筑物的最高点,设计一种测量建筑物高度 AB 的方法。分析:求AB 长的关键是先求 AE,在ACE 中,如能求出 C 点到建筑物顶部 A 的距离 CA,再测出由 C 点观察 A 的仰角,就可以计算出 AE的长。解析:选择一条水平基线 HG,使 H、G、B 三点在同一条直线上。由在 H、G 两点用测角仪器测得A 的仰角分别是 、 ,CD = a,测角仪器的高是 h,那么,在ACD 中,根据正弦定理可得AC = AB = AE + h = ACsin+ h2= + h例题 4、 如图,一艘海轮从 A 出发,沿北偏东 75 的方向航行 67.5 n mile 后到达海岛 B,然后从 B 出发,沿北偏东 32 的方向航行 54.0 n mile 后达到海岛 C.如果下次航行直接从 A 出发到达 C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到 0.1 ,距离精确到0.01n mile)解析:在ABC 中,ABC=180 - 75 + 32 =137 ,根据余弦定理,AC= = ≈113.15根据正弦定理, = sinCAB = = ≈0.3255,所以 CAB =19.0 , 75 - CAB =56.0答:此船应该沿北偏东 56.1 的方向航行,需要航行 113.15n mile3