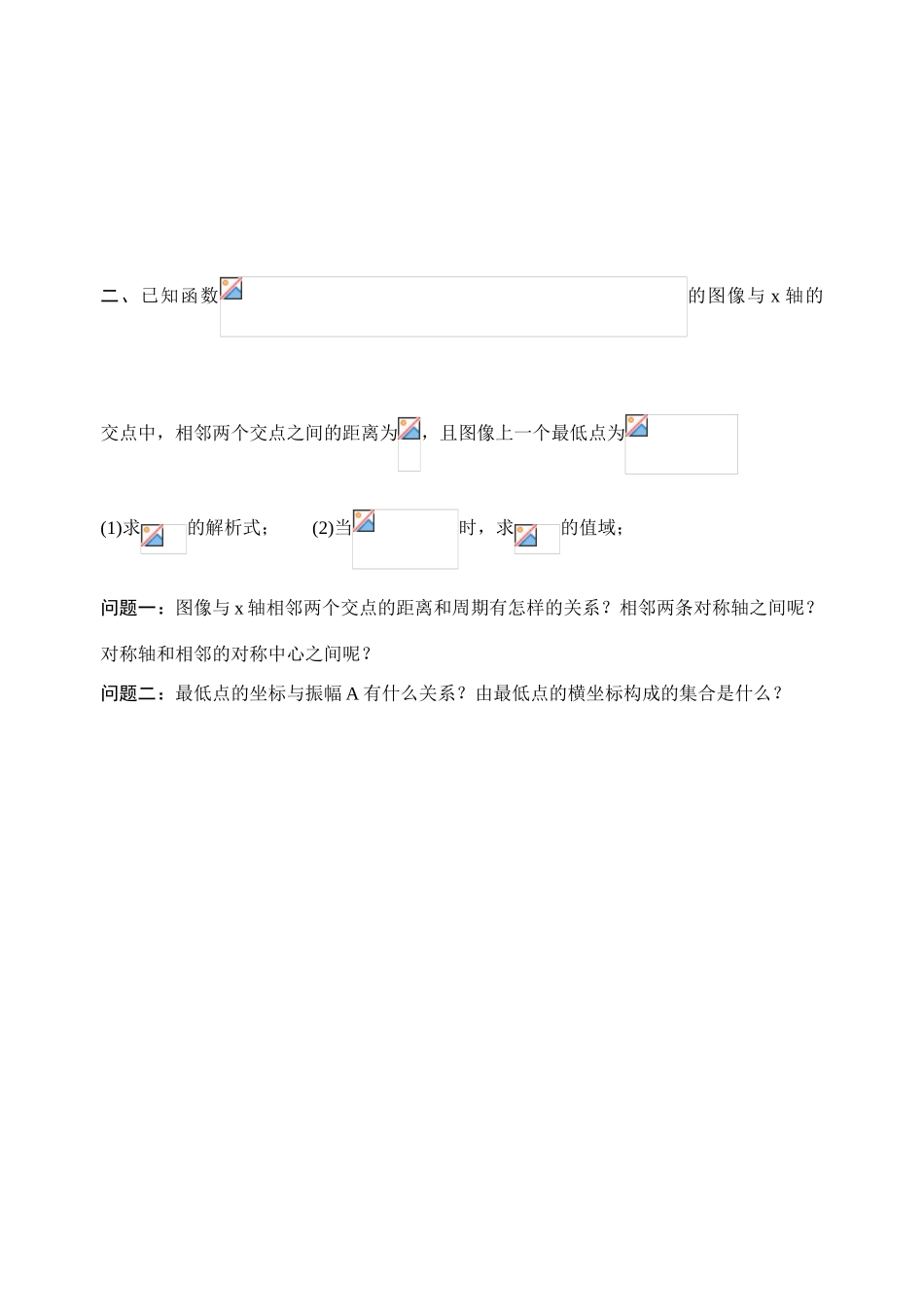
8,1 求正弦型函数的解析式问题导学案学习目标:能够正确求正弦型函数的解析式;学习重点:利用五点求 A,,及 K学习过程:(一)预习,复习巩固完成下列题目:1、函数的对称轴方程可能是( )A、 B、 C、 D、2、把函数的图像上所有点向左平行移动个单位长度,再把所得图像上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图像表示的函数是( )A、 B、C、 D、3、若函数在区间上单调递增,在区间上单调递减,则等于( )A、3 B、2 C、 D、4、已知,,则的图像( )主备________A、与的图像相同 B、向右平移个单位,得到的图像C、与的图像关于 y 轴对称 D、向左平移个单位,得到的图像 课内探究一:求正弦型函数的解析式一、观察函数的部分图像,则( )A、 B、C、 D、跟踪训练:某地一天从 6 时至 14 时的温度变化曲线近似满足函数;(1)求这段时间的最大温差; (2)写出这段曲线的函数解析式;6 10 14 x 时间y 温度302010O二、已知函数的图像与 x 轴的交点中,相邻两个交点之间的距离为,且图像上一个最低点为(1)求的解析式; (2)当时,求的值域;问题一:图像与 x 轴相邻两个交点的距离和周期有怎样的关系?相邻两条对称轴之间呢?对称轴和相邻的对称中心之间呢?问题二:最低点的坐标与振幅 A 有什么关系?由最低点的横坐标构成的集合是什么?跟踪训练:已知函数上的一个最高点的坐标 为, 此 点 到 右 侧 相 邻 最 低 点 间 的 连 线 与 x 轴 的 交 点 为,(1)求函数的解析式;(2)画出函数在一个周期内的图像;(3)写出函数的单调区间;正弦型函数的性质限时训练1、若函数是偶函数,则的一个值是( )A、 B、 C、 D、2、设,函数向右平移个单位后,与原图像重合,则的最小值是( )A、 B、 C、 D、33、下列函数中,周期为,且在区间上为减函数的是( )A、B、C、D、4、设函数,则下列结论正确的是( )A、的图像关于直线对称B、的图像关于点对称C、把的图像向左平移个单位,得到一个偶函数的图像D、的最小正周期为,且在区间上为增函数5、函数的图像的一条对称轴方程为( )A、 B、 C、 D、6、函数的一个单调递增区间是( )A、 B、 C、 D、7、函数的图像关于原点成中心对称,则等于( )A、 B、 C、 D、8、已知函数的最小正周期为,为了得到函数的图像,只要将函数的图像向 平移 各单位长度。9、关于函数有下列命题:① 由,可得必是的整数倍;②的表达式可以改写为③的图像关于点对称;④的图像关于直线对称;其中正确的是 10、设的最小正周期为;(1)求; (2)求的解析式; (3)若,求