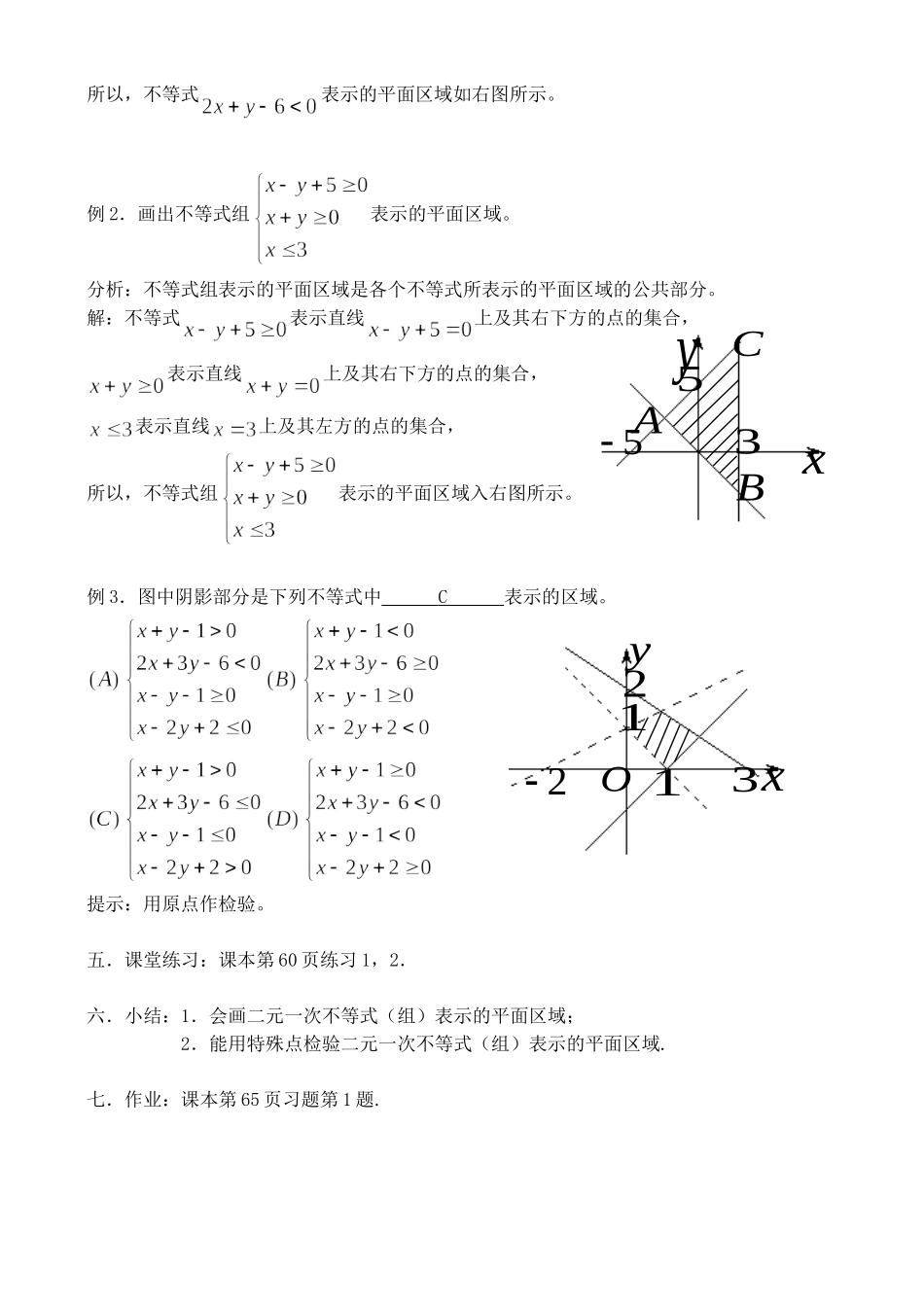
简单的线性规划(1)一.课题: 二.教学目标:1.了解二元一次不等式表示平面区域,会用,或检验不等式()表示的平面区域;2.会画出二元一次不等式(组)表示的平面区域.三.教学重、难点:怎样用二元一次不等式(组)表示平面区域;怎样确定不等式 ()表示直线的哪一侧区域.四.教学过程:(一)引入:点集是以二元一次方程的解为坐标的集合,它是一条直线,经过和,那么点集在平面直角坐标系中表示什么图形呢?(二)新课讲解:1.尝试、猜想、证明在平面直角坐标系中,所有的点被直线分成三类:一类是在直线上;二类是在直线的右上方的平面区域内;三类是在直线的左下方的平面区域内.对于任意一个点,把它的坐标代入,可得到一个实数,或等于,或大于,或小于,此时,可引导学生尝试在什么情况下,点在直线上、在直线右上方、在直线左下方?猜想结论:对直线右上方的点,;对直线左下方的点,.xyO100( , )P x y1 0xy 1证明结论:如图,在直线上任取一点,过作平行于轴的直线,在此直线上点右侧的任意一点,都有,,所以,,,因为点为直线上任意一点,所以,对于直线右上方任意点,都有,同理对于直线左下方任意点,都有,所以,结论得证.2.得出结论一般地,二元一次不等式在平面直角坐标系中表示某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式所表示的平面区域时,此区域应包括边界直线,则把直线画成实线.说明:由于直线同侧的所有点的坐标代入,得到实数符号都相同,所以只需在直线某一侧取一个特殊点,从的正负即可判断表示直线哪一侧的平面区域.特别地,当时,通常把原点作为此特殊点.(三)例题分析:例 1.画出不等式表示的平面区域.解:先画出直线(虚线), 取原点代入,∵, ∴原点在表示的平面区域内 ,xy所以,不等式表示的平面区域如右图所示。例 2.画出不等式组表示的平面区域。分析:不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分。解:不等式表示直线上及其右下方的点的集合,表示直线上及其右下方的点的集合,表示直线上及其左方的点的集合,所以,不等式组表示的平面区域入右图所示。例 3.图中阴影部分是下列不等式中 C 表示的区域。提示:用原点作检验。五.课堂练习:课本第 60 页练习 1,2.六.小结:1.会画二元一次不等式(组)表示的平面区域;2.能用特殊点检验二元一次不等式(组)表示的平面区域.七.作业:课本第 65 页习题第 1 题.xyABC355xyO21123