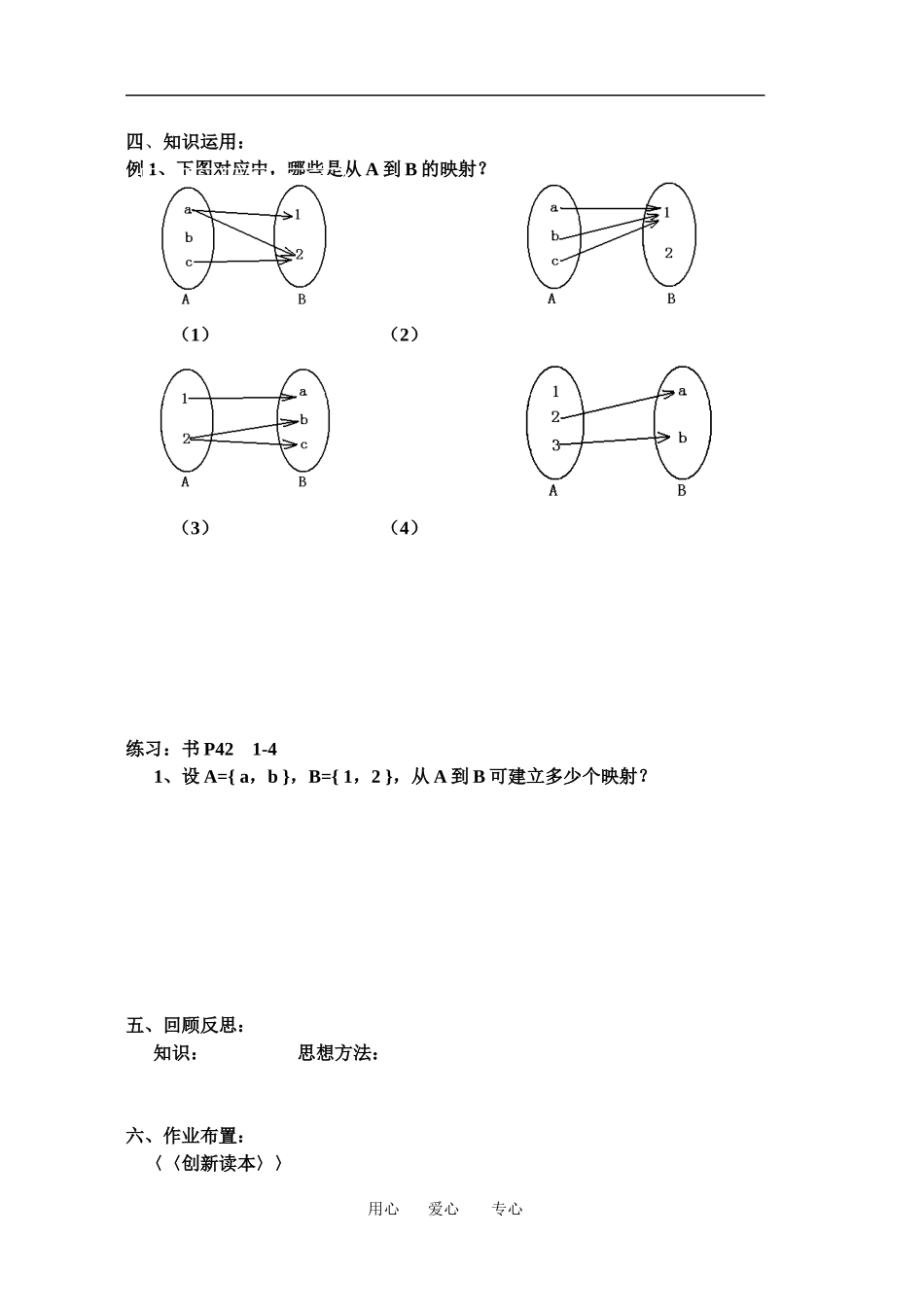
映射的概念教学目标:了解映射的概念,进一步了解函数是非空数集的映射,培养学生观察、分析、比较能力。 教学重点:映射的概念 教学难点:映射的概念教学过程:一、问题情境:观察下面一些对应,是否满足单值对应?(1)A={x| x 为高一(1)班学生} B={x| x>0 } f:A→B 写出每位学生体重数(2)A={P| P 为坐标平面内的点} B={(x,y)| x∈R,y∈R } f:A→B 每一点与其坐标对应(3)A={x| x 为平面 M 内三角形} B={x| x 为平面 M 内圆 } f:A→B 画出三角形外接圆二、学生活动: 上述对应能否称为从 A 到 B 的函数?说明理由。三、知识建构: 映射:思考:函数与映射有何联系、区别?用心 爱心 专心四、知识运用:例 1、下图对应中,哪些是从 A 到 B 的映射? (1) (2) (3) (4)练习:书 P42 1-4 1、设 A={ a,b },B={ 1,2 },从 A 到 B 可建立多少个映射?五、回顾反思:知识: 思想方法:六、作业布置:〈〈创新读本〉〉用心 爱心 专心映射的概念教学目标:了解映射的概念,进一步了解函数是非空数集的映射,培养学生观察、分析、比较能力。 教学重点:映射的概念 教学难点:映射的概念教学过程:一、问题情境:观察下面一些对应,是否满足单值对应?(1)A={x| x 为高一(1)班学生} B={x| x>0 } f:A→B 写出每位学生体重数(2)A={P| P 为坐标平面内的点} B={(x,y)| x∈R,y∈R } f:A→B 每一点与其坐标对应(3)A={x| x 为平面 M 内三角形} B={x| x 为平面 M 内圆 } f:A→B 画出三角形外接圆二、学生活动: 上述对应能否称为从 A 到 B 的函数?说明理由。析:观察对应关系三、知识建构: 映射:思考:函数与映射有何联系、区别?用心 爱心 专心四、知识运用:例 1、下图对应中,哪些是从 A 到 B 的映射? (1) (2) (3) (4)解析:(1)不是,a 一对多,b 没有对应(2)是,多对一(3)不是,2 一对多(4)不是,a 一对多,1 没有对应小结:映射的定义练习:书 P42 1-4 1、设 A={ a,b },B={ 1,2 },从 A 到 B 可建立多少个映射?解析:列举法从 A 到 B 可建立 2×2=4 个映射变式:1、设 A={ a,b,c },B={ 1,2,3 },从 A 到 B 可建立多少个映射?(答案:3×3=9 个)注:请结合书本及《创新》多举例子,多做练习,便于学生对映射定义的掌握。五、回顾反思:知识:映射的定义方法:定义法、列举法思想:特殊到一般六、作业布置:〈〈创新读本〉〉用心 爱心 专心用心 爱心 专心