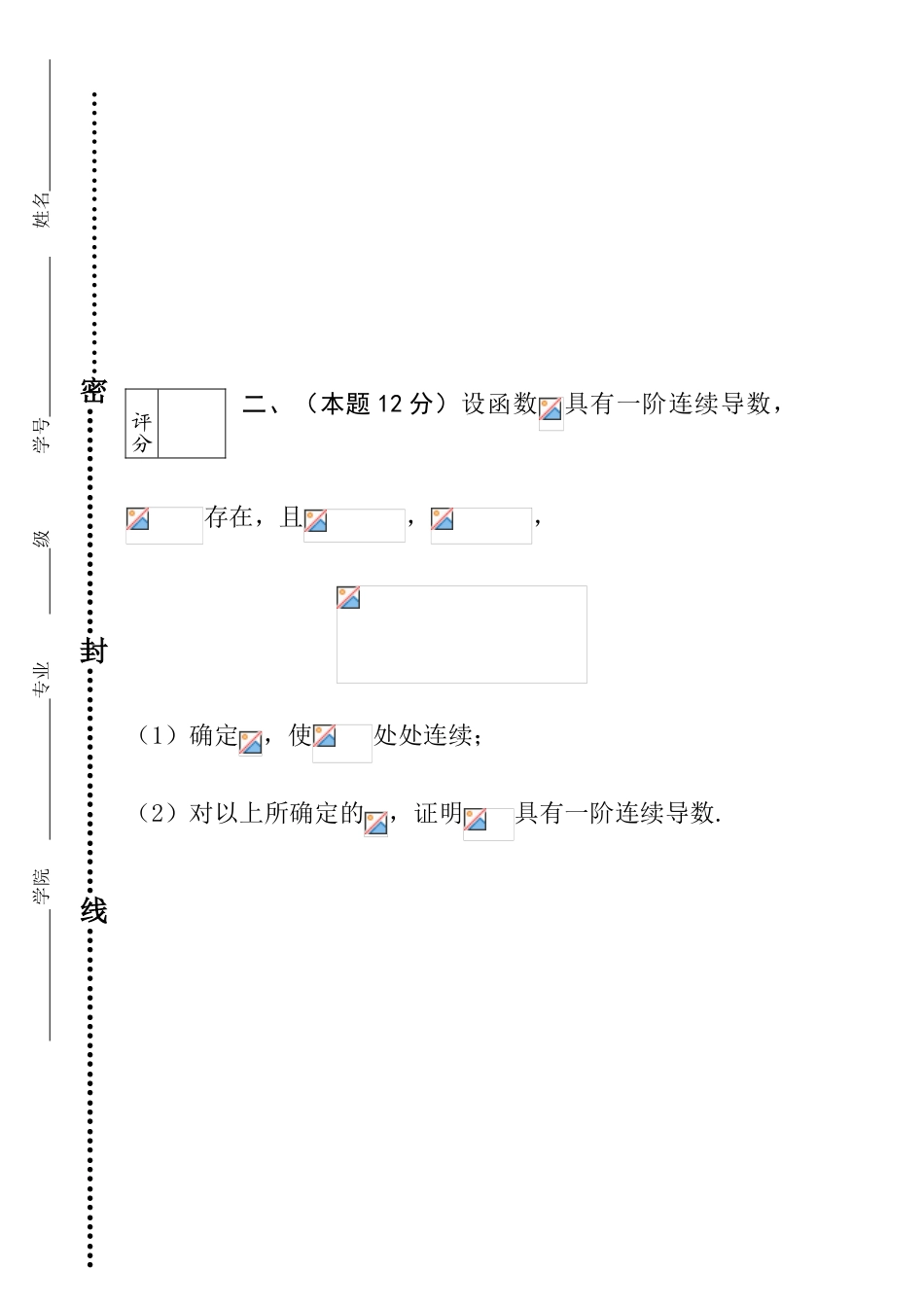
一、计算下列各题(要求写出重要步骤)(本题共4 小题,每小题 7 分,共 28 分) (1)计算 (2) 计算广义积分 (3) 设确定,其中具有一阶连续偏导数, 求(4) 计算 评分…………………………密……………………封……………………线……………………………… 学院 专业 级 学号 姓名 二、(本题 12 分)设函数具有一阶连续导数,存在,且,,(1)确定,使处处连续;(2)对以上所确定的,证明具有一阶连续导数. 评分…………………………密……………………封……………………线……………………………… 学院 专业 级 学号 姓名 三、(本题 12 分)设当时, 可微函数满足条件,且,试证: 当时, 有成立.评分四、(本题 12 分)设在上可导,且,证明:,使. 评分 学院 专业 级 学号 姓名 …………………………密……………………封……………………线………………………………五、(本题 12 分)设 (1)证明:当时幂级数收敛;(2)求上述幂级数在内的和函数.评分六、(本题 12 分)( a ) ( 非 理 工 组 做 ) 设, , 其 中连 续 , 求.(b)(理工组做) 设函数在内有一阶连续导数, 是上半平面内的有向分段光滑曲线,其起点,终点为, 记,(1)证明:曲线积分与路径 无关; (2)当时,求 的值.七、(本题 12 分)设锥面平面评分评分 学院 专业 级 学号 姓名 …………………………密……………………封……………………线………………………………点是 上到 距离最小的点,求以点为中心与 相切的球面方程与切点坐标.