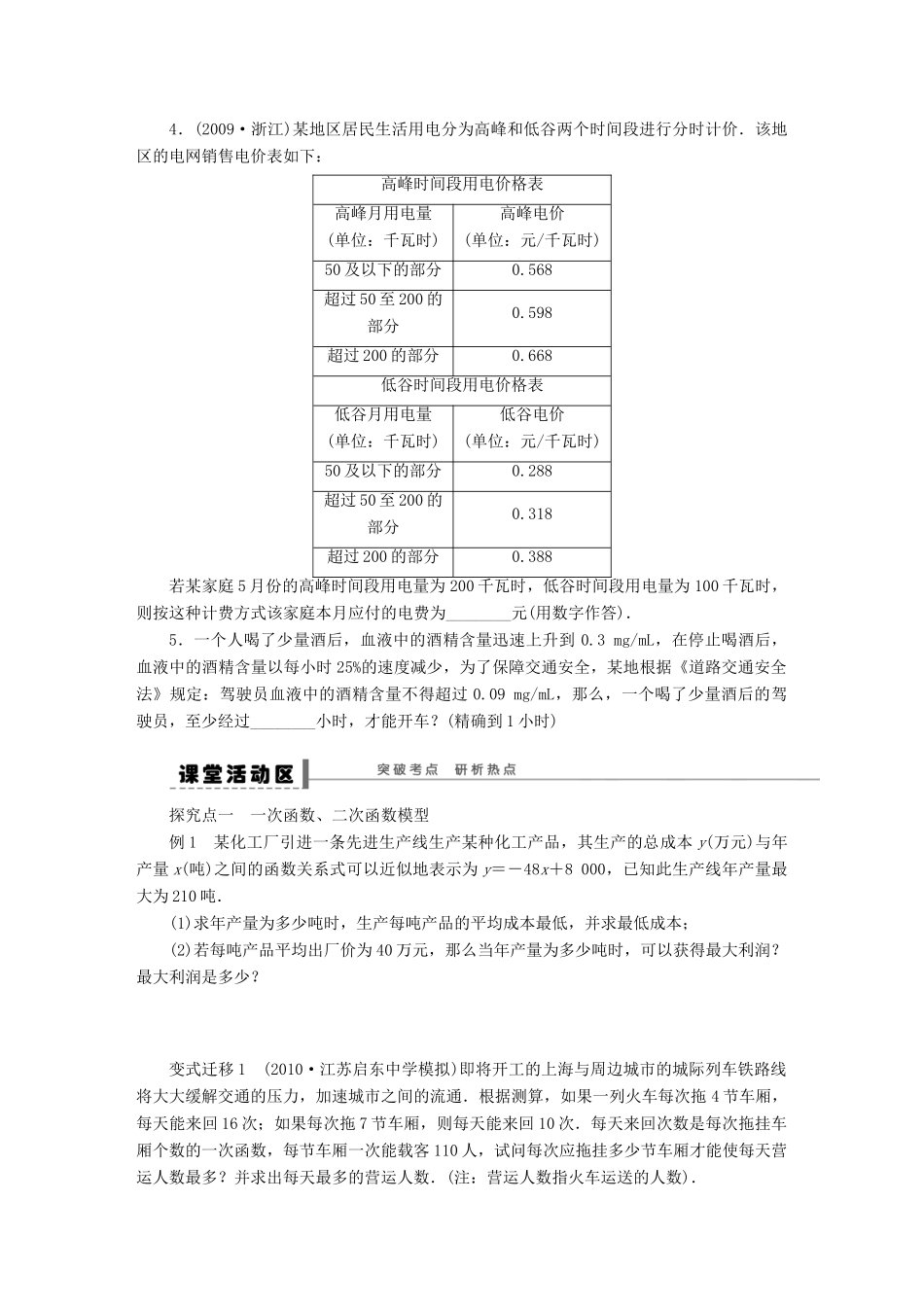
学案 12 函数模型及其应用导学目标: 1.能够应用函数知识构造函数模型,解决简单的实际生活中的优化问题.2.能利用函数与方程、不等式之间的关系,解决一些简单问题.自主梳理1.几种常见函数模型(1)一次函数模型:y=kx+b(k、b 为常数,k≠0);(2)反比例函数模型:y=+b(k、b 为常数,k≠0);(3)二次函数模型:y=ax2+bx+c(a、b、c 为常数,a≠0),二次函数模型是高中阶段应用最为广泛的模型,在高考的应用题考查中是最为常见的;(4)指数函数模型:y=kax+b(k、a、b 为常数,k≠0,a>0 且 a≠1);(5)对数函数模型:y=mlogax+n(m、n、a 为常数,m≠0,a>0 且 a≠1);(6)幂函数模型:y=axn+b(a、b、n 为常数,a≠0,n≠0);(7)分式函数模型:y=x+(k>0);(8)分段函数模型.2.解应用题的方法和步骤用框图表示如下:自我检测1. 某工厂八年来某种产品总产量 C 与时间 t(年)的函数关系如图所示,下列四种说法:① 前三年中产量增长速度越来越快;② 前三年中产量增长的速度越来越慢;③ 第三年后,这种产品停止生产;④ 第三年后,年产量保持不变.其中说法正确的是________.(填上正确的序号)2.(2011·广州模拟)计算机的价格大约每 3 年下降,那么今年花 8 100 元买的一台计算机,9 年后的价格大约是________元.3.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为 L1=5.06x-0.15x2和 L2=2x,其中 x 为销售量(单位:辆).若该公司在这两地共销售 15 辆车,则能获得的最大利润为________.4.(2009·浙江)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:高峰时间段用电价格表高峰月用电量(单位:千瓦时)高峰电价(单位:元/千瓦时)50 及以下的部分0.568超过 50 至 200 的部分0.598超过 200 的部分0.668低谷时间段用电价格表低谷月用电量(单位:千瓦时)低谷电价(单位:元/千瓦时)50 及以下的部分0.288超过 50 至 200 的部分0.318超过 200 的部分0.388若某家庭 5 月份的高峰时间段用电量为 200 千瓦时,低谷时间段用电量为 100 千瓦时,则按这种计费方式该家庭本月应付的电费为________元(用数字作答).5.一个人喝了少量酒后,血液中的酒精含量迅速上升到 0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时 25%的速度减少,为了保障交通安全,某地根据《道路交通安全法》规定:驾驶员血液中的酒精含量不得超过 0.09 mg/mL...