高中数学-立体几何大题 (1)

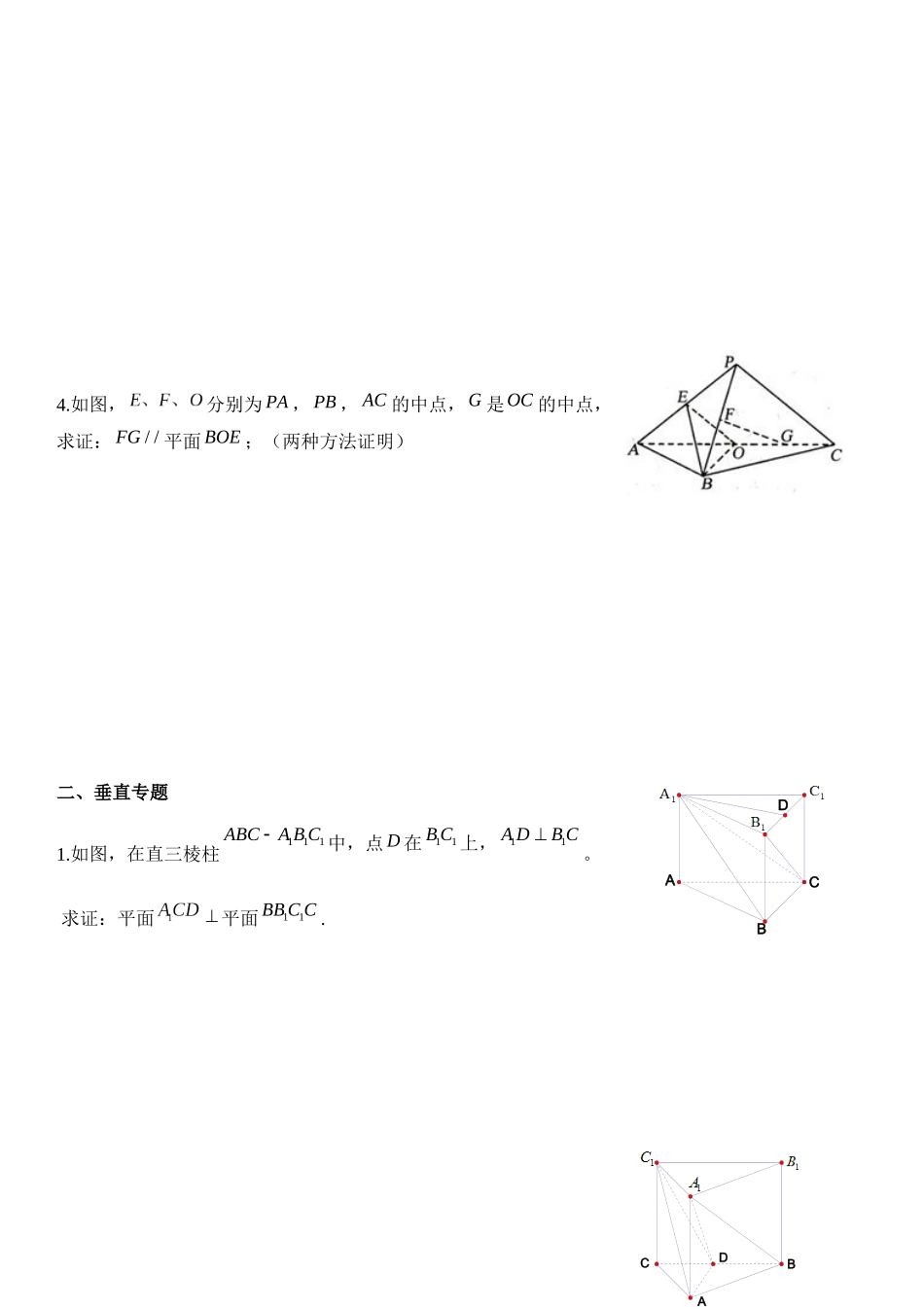
一、线面平行专题1.如图，在直三棱柱111ABCA B C中， E 、 F 分别是1A B 、1AC 的中点，求证： EF∥平面 ABC； 2.如图，正三棱柱中，是的中点， 求证：平面．（两种方法证明）3．如图，在底面为平行四边行的四棱锥中，点是的中点.求证：平面；（两种方法证明）ACBDABCEFPABCDE4.如图，分别为 PA ， PB ， AC 的中点，G 是OC 的中点，求证：/ /FG平面 BOE ；（两种方法证明）二、垂直专题1.如图，在直三棱柱111ABCA B C中，点 D 在11B C 上，11A DB C。 求证：平面 平面11BB C C .ACBDABCD2.如图，正三棱柱中，是的中点，．求证：直线； 3.如图，四棱锥 PABCD的底面是正方形， PDABCD 底面，点 E 在棱 PB 上. 求证：平面 AECPDB 平面； 4.如图，直三棱柱111ABCA B C中，AB=1，13ACAA，∠ABC=600.求证：1ABAC； PBACDEBCADBCABa111A DB C5. 直三棱柱中，，，分别是的中点，求证：平面； 6.如图，在三棱锥 PABC中，⊿ PAB 是等边三角形，∠PAC=∠PBC=90º。 求证：AB⊥PC 三、线面角和距离1.如图，正三棱柱中，是的中点，．求点到平面的距离；（两种方法求解） ACBDACBMNPBCA2. 如 图 ， 四 棱 锥 PABCD的 底 面 是 正 方 形 ， PDABCD 底面，2PDAB且 E 为 PB 的中点时，求 AE 与平面 PDB 所成角的大小.3.如图， DC 平面 ABC ，/ /EBDC ，120ACB，22ACBCEBDC ，,P Q 分别为,AE AB 的中点．求 AD 与平面 ABE 所成角的正弦值．4.如图 3，在正三棱柱111ABCA B C中，AB=4, 17AA ,点 D 是 BC 的中点，点 E 在 AC 上，且 DE1A E.PBACDEACDBEQPBACDE（Ⅰ）证明：平面1A DE  平面11ACC A ; （Ⅱ）求直线 AD 和平面1A DE 所成角的正弦值。（两种方法求解）5.如图，在四棱锥中，侧面底面，侧棱,底面为直角梯形，其中，. ( ) Ⅰ 求异面直线与所成角；( ) Ⅱ 求与平面所成的角； ()Ⅲ 求点到平面的距离.PABCD6.如图，在正三棱柱111ABCA B C中，，D 是11A B 的中点，点 E 在11AC 上，且 DEAE。7.（1）证明平面 ADE 平面11ACC A ； 8.（2）求直线 AD 和平面 ABC 1 所成的角。 四、二面角1.如图，直三棱柱111ABCA B C中， AB=1，13ACAA，ABC=60∠0.( )Ⅰ 证明：1ABAC；（Ⅱ）求二面角 A—1AC —B。 ACBMNABCDEBAC2....