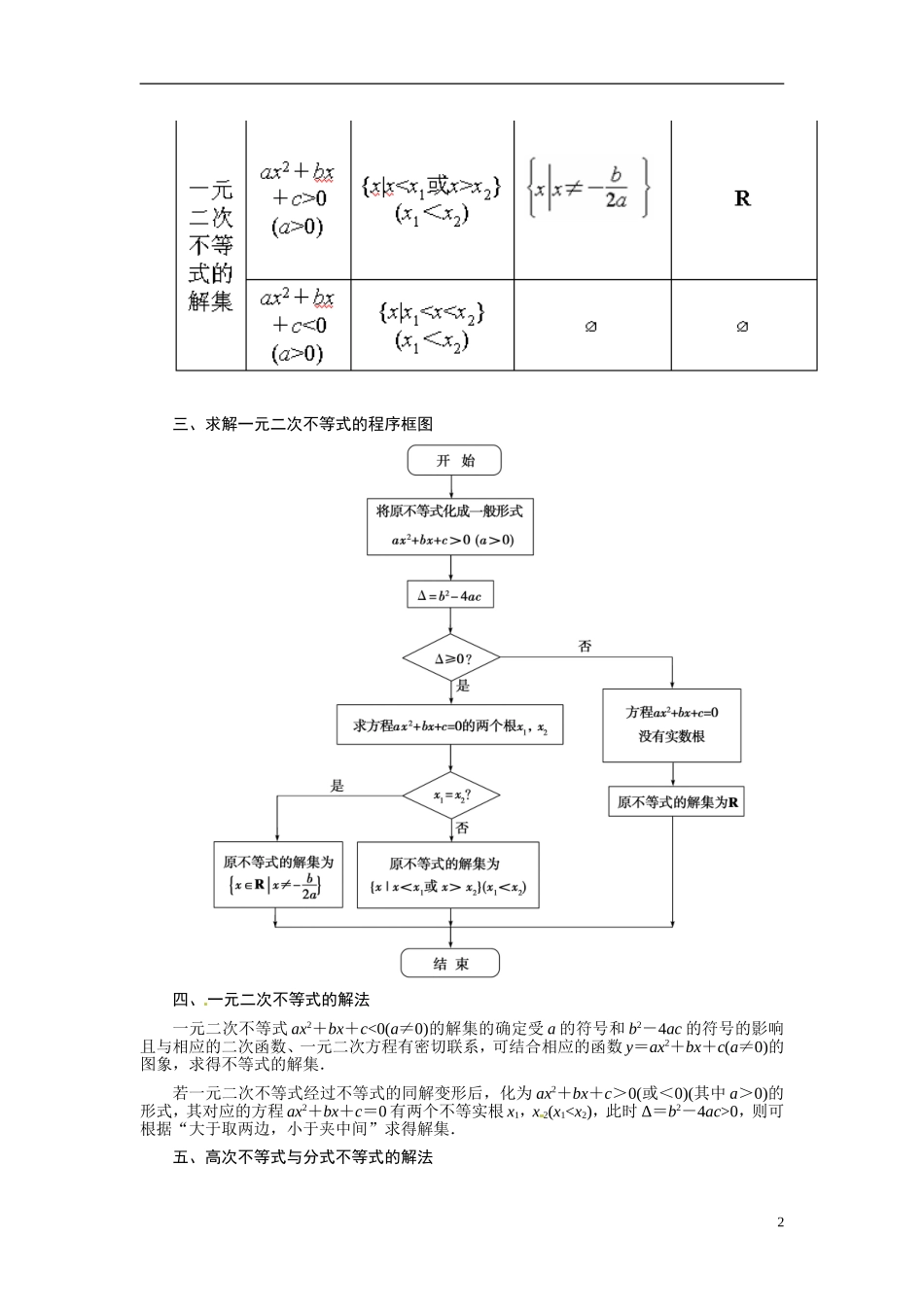
第二节一元二次不等式及其解法1.会从实际情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.知识梳理一、一元二次不等式的概念1.我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式.2.使某个一元二次不等式成立的 x 的值叫做这个一元二次不等式的解,一元二次不等式所有的解组成的集合叫做一元二次不等式的解集.二、二次函数、一元二次方程与一元二次不等式的关系1三、求解一元二次不等式的程序框图四、一元二次不等式的解法一元二次不等式 ax2+bx+c<0(a≠0)的解集的确定受 a 的符号和 b2-4ac 的符号的影响且与相应的二次函数、一元二次方程有密切联系,可结合相应的函数 y=ax2+bx+c(a≠0)的图象,求得不等式的解集.若一元二次不等式经过不等式的同解变形后,化为 ax2+bx+c>0(或<0)(其中 a>0)的形式,其对应的方程 ax2+bx+c=0 有两个不等实根 x1,x 2(x10,则可根据“大于取两边,小于夹中间”求得解集.五、高次不等式与分式不等式的解法21.高次不等式的解法:先将最高次项的系数化为正数,然后分解因式,将相应方程的所有根画在数轴上,采取“数轴标根”法(或称穿针引线法)得出不等式的解集.数轴标根法的操作过程:(1)把不等式变形为一边是一次因式的积,另一边是 0 的形式;(2)各因式中 x 的系数全部变为 1,约去偶次因式;(3)把各个根从小到大依次排好标出,从数轴最左端向右端依次取根判断,并“引线”;(4)严格检查因式的根(特别是约去的偶次因式的根)是否在解集内.2.分式不等式的解法:将分式不等式转化为整式不等式,通过“穿针引线”法得出不等式的解集.>0(<0)可转化为 f(x)g(x)>0(<0);≥0(≤0)可以转化为基础自测1.不等式 x2>x 的解集是( )A.(-∞,0)B.(0,1)C.(1,+∞)D.(-∞,0)∪(1,+∞)解析:由 x2>x 得 x(x-1)>0,所以解集为(-∞,0)∪(1,+∞).故选 D.答案:D2.(2013·广州一模)“m<2”是“一元二次不 等式 x2+mx+1>0 的解集为 R”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:一元二次不等式 x2+mx+1>0 的解集为 R 等价于:Δ=m2-4<0,即-2<m<2.故选 B.答案:B3.(2013·上海卷)不等式<0 的解为_____...