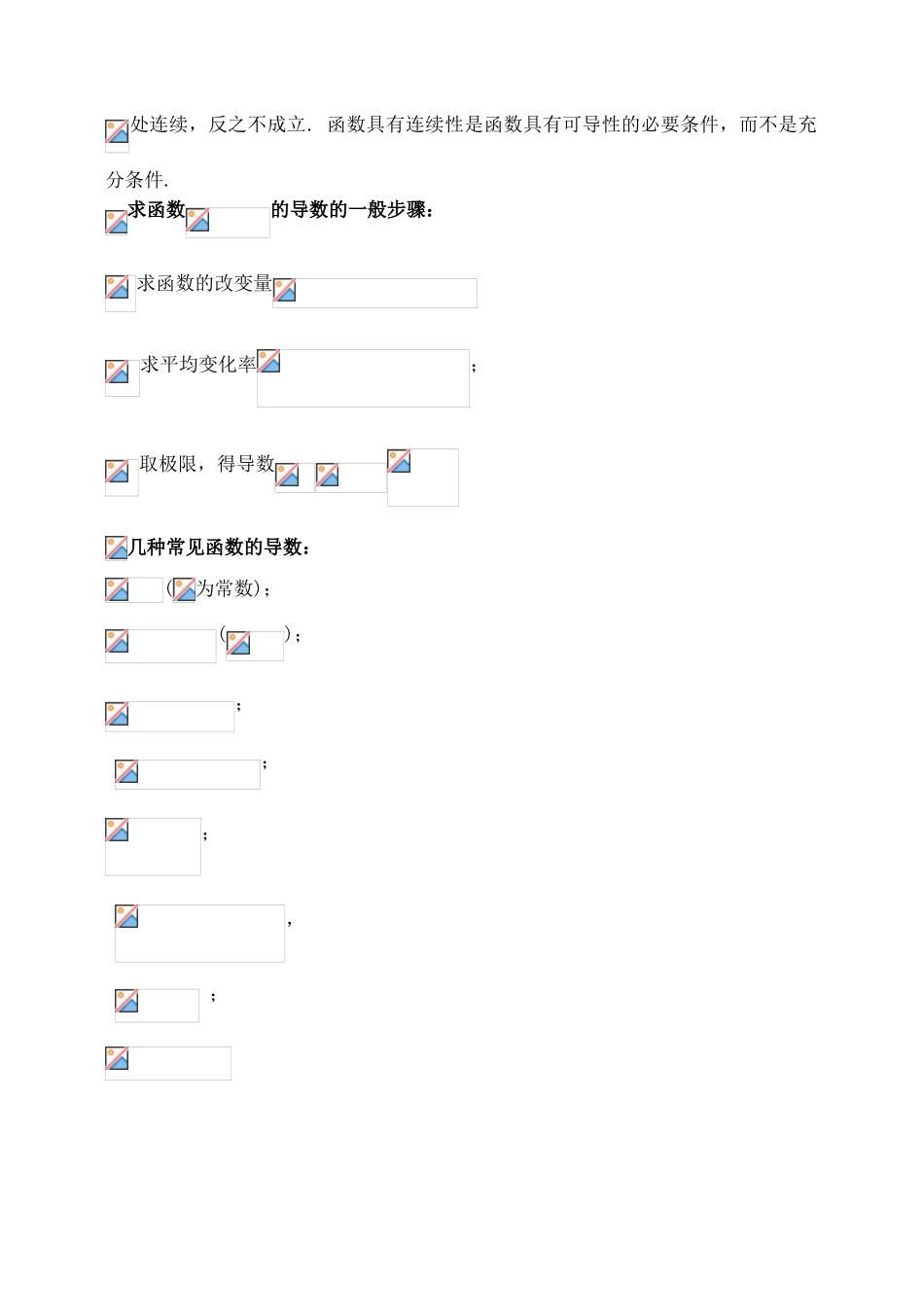
吉林省东北师范大学附属中学 2015 届高三数学第一轮复习(知识梳理+题型探究+方法提升+课后作业)导数的概念及运算导学案 文知识梳理:(阅读选修教材 2-2 第 2 页—第 21 页)1、 导数及有关概念:函数的平均变化率:设函数在处附近有定义,当自变量在处有增量时,则函数相应地有增量,如果时,与的比(也叫函数的平均变化率)有极限即无限趋近于某个常数,我们把这个极限值叫做函数在处的导数,记作,即在定义式中,设,则,当趋近于时,趋近于,因此,导数的定义式可写成.几何意义:几 何 意 义 是 曲 线上 点 () 处 的 切 线 的 斜 率 . 因 此 , 如 果在 点可 导 , 则 曲 线在 点 () 处 的 切 线 方 程 为 导函数(导数):如果函数在开区间内的每点处都有导数,此时对于每一个,都对应着一个确定的导数,从而构成了一个新的函数, 称这个函数为函数在开区间内的导函数,简称导数,也可记作,即==说明 :导数与导函数都称为导数,这要加以区分,求一个函数的导数,就是求导函数,求一个函数在给定点处的导数,就是求导函数值.可导: 如果函数在开区间内每一点都有导数,则称函数在开区间内可导可导与连续的关系:如果函数在点处可导,那么函数在点处连续,反之不成立. 函数具有连续性是函数具有可导性的必要条件,而不是充分条件.求函数的导数的一般步骤:求函数的改变量求平均变化率;取极限,得导数 几种常见函数的导数:(为常数);();; ;; , ; 二、题型探究: 探究一.用导数的定义求函数在某一点处的导函数值。例1:已知,求(- )探究二.导数的几何意义例 2:已知曲线 .(1)、求曲线在点 P(2,4)处的切线方程;(y=4x-4)(2)、求过点 P(0,0)的曲线的切线方程;(y=x)(3)、求斜率为 1 的曲线的切线方程。(y=x-2;y=x+ )探究三:导数的运算:例 4:求下列函数的导数(1)、sin2x(2)、(3)、探究五:求导运算后求切线方程例 5:已知函数(1)、若 a=1,点 P 为曲线上的一个动点,求以点 p 为切点的切线的斜率取最小值时的切线方程;(y=x+ )(2)、求函数在(0,+)上为单调增函数,试求满足条件的最大整数 a。(a=1)四、反思感悟: 五、课时作业一、选择题1.对于上可导的任意函数,若满足≥,则必有(D) ≤ ≥ 1、 设函数,在上均可导,且,则当时,有(C) 3、的导函数的图象如图所示,则的图象最有可能的是(C) 4、,,,…,,,则 =(A) 5、若曲线的...