山东省泰安市肥城市第三中学高中数学 2.2.2面面平行的判定学案 新人教A版必修2

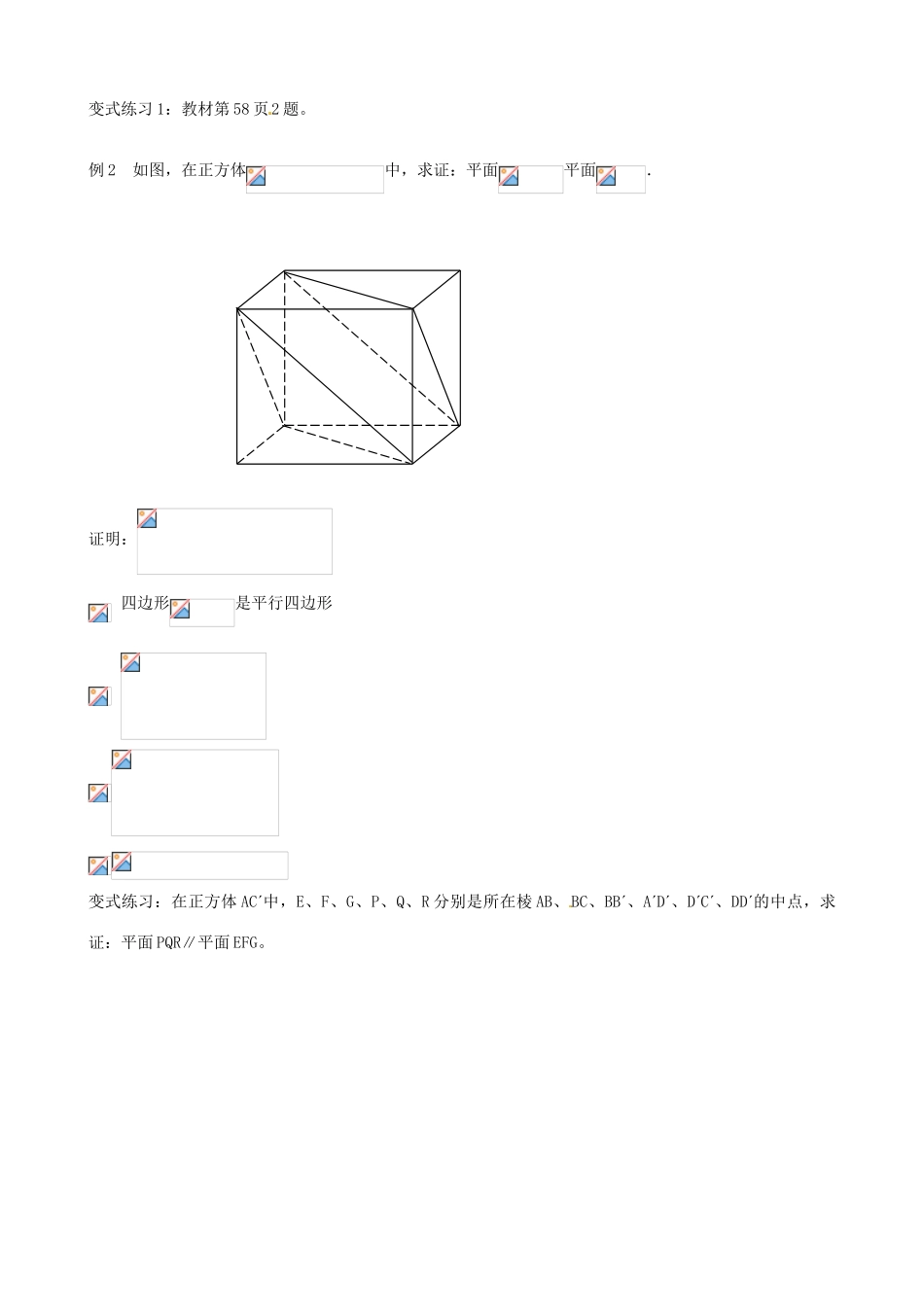
山东省泰安市肥城市第三中学高一数学人教 A 版必修 2 学案：2.2.2 面面平行的判定（教案）学习内容学习指导即时感悟【情境导入】引导学生观察、思考教材第 57 页的观察题，导入本节课所学主题。【自主·合作·探究】上节课我们研究了两个平面的位置关系，具有什么条件的两个平面是平行的呢?1、问题：（1）平面 β 内有一条直线与平面 α 平行，α、β 平行吗？（2）平面 β 内有两条直线与平面 α 平行，α、β 平行吗？通过长方体模型，引导学生观察、思考、交流，得出结论。（3）平面 α 内有无数条直线与平面 β 平行，则 α∥β，对吗? （4）、如下图，平面内有两条相交直线与平面平行，情况如何？两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。符号表示：类比平面中线线平行得出判断两平面平行的方法有三种：（1）用定义；（2）判定定理；（3）垂直于同一条直线的两个平面平行。二、典型例题例 1 课本 P57：已知正方体 ABCD-,求证：平面//平面。分析：要证面面平行需转化为线面平行，同理证明：因为 ABCD-为正方体，所以 ，又，所以 ，，所以为平行四边形。所以。又,,由直线与平面的判定定理得，同理，又，所以平面。变式练习 1：教材第 58 页2 题。例 2 如图，在正方体中，求证：平面平面．证明： 四边形是平行四边形变式练习：在正方体 AC中，E、F、G、P、Q、R 分别是所在棱 AB、BC、BB、AD、DC、DD的中点，求证：平面 PQR∥平面 EFG。从情境抽象出图形语言ABCDABCDFQEGRP点评：例子的给出，有利于学生掌握该定理的应用学生先独立完成后，教师指导讲评。分析：欲证面面平行思想就是转化为线面平行继而转化为平面中的线线平行点评：本题进一步加深了空间问题平面化的思想。【当堂达标】1、判断下列命题是否正确（1）若平面内的两条直线分别与平面平行，则平面与平面平行；（2）若平面内有无数条直线分别与平面平行，则平面与平面平行；（3）平行于同一直线的两个平面平行；（4）两个平面分别经过两条平行直线，这两个平面平行；（5）过已知平面外一条直线，必能作出与已知平面平行的平面．2、若 a，b 为异面直线，则与的位置关系_____________. （D）不可能有3、教材 62 第 7 题【反思·提升】【拓展·延伸】1．设直线 l, m, 平面 α,β,下列条件能得出 α∥β 的有 ( )①lα,mα,且 l∥β,m∥β；② lα,mα,且 ...