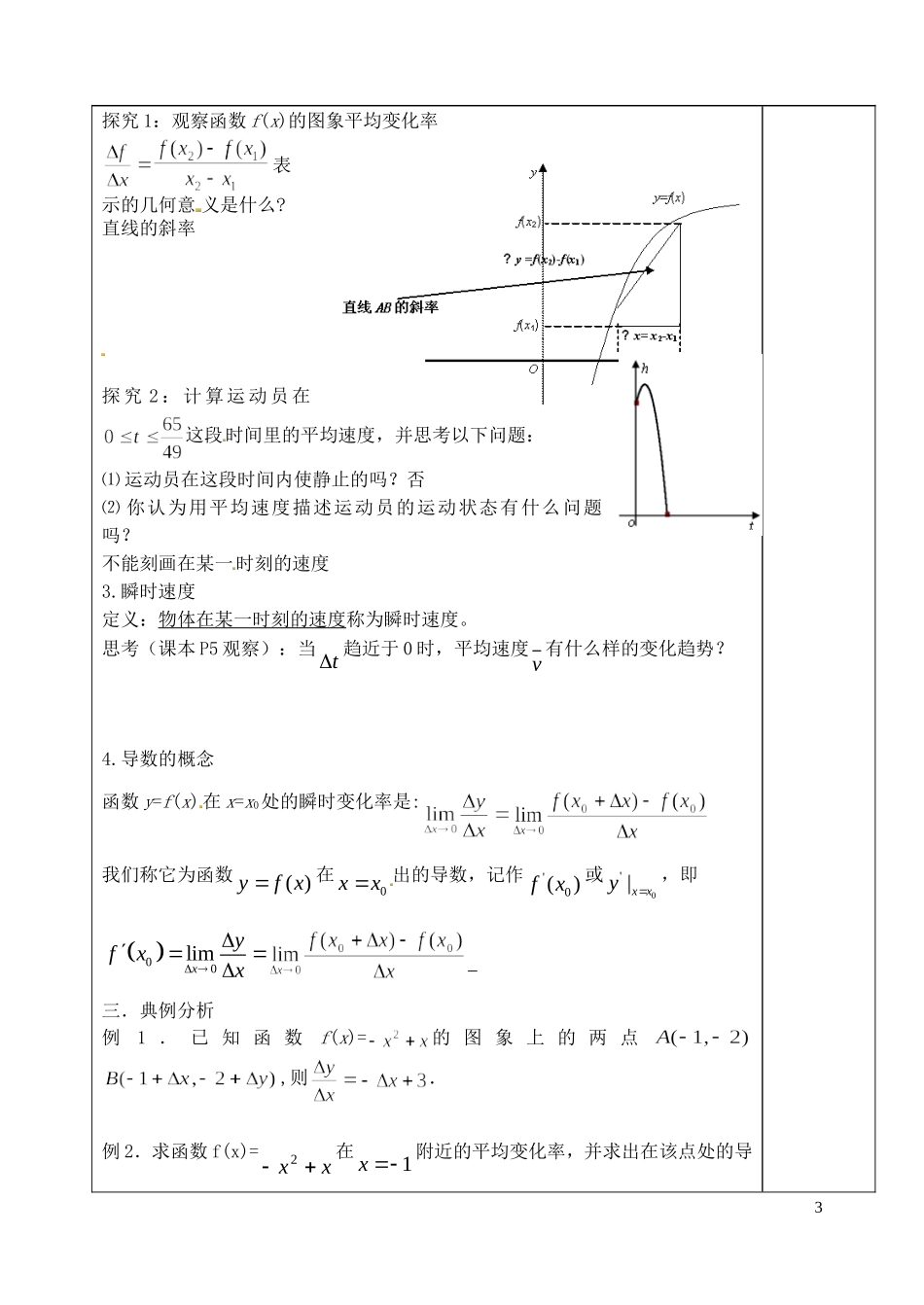
山东省泰安市肥城市第三中学高中数学 变化率问题与导数的概念学案 新人教 A 版选修 2-2学习内容学 习 指 导即时感悟【学习目标】1.理解平均变化率与导数的概念;了解平均变化率的几何意义、瞬时速度、瞬时变化率的概念;会求函数在某点处附近的平均变化率及导数。2.用探究的方法由平均变化率探求瞬时变化率,推出导数的概念,理 解导数的内涵。3.培养学生科学严谨的探索精神。【学习重点】平均变化率的概念、函数在某点处附近的平均变化率;导数的概念。【学习难点】平均变化率的概念、导数的概念。【预习新知】1、对于函数 yf x,当自变量 x 从1x 变到2x 时,函数值从 1f x变到2f x,则称式子为 yf x从1x 到2x 的平均变化率,简记作:。2、函数 xfy 的平均变化率的几何意义是指函数 xfy 图象上两点 111,xfxP、 222,xfxP连线的 斜率 3、函数 yf x在0xx处的瞬时变化率是函数 f x 从0x 到0xx 的平均变化率在0x 时的极限,即0limxyx 。4、函数 yf x在0xx处的瞬时变化率称为函数 yf x在0xx处的导数,记作,即 00limxyfxx 5、总结求导数的步骤:一差二比三极限【自主﹒合作﹒探究】一、引入导数是微积分的核心概念之一,它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度.二、问题提出问题 1 气球膨胀率 我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢?1(1)当 V 从 0 增加到 1 时,气球半径增加了气球的平均膨胀率为(2)当 V 从 1 增加到 2 时,气球半径增加了气球的平均膨胀率为思考:当空气容量从 V1增加到 V2时,气球的平 均膨胀率是多少? 问题 2 高台跳水在高台跳 水运动中,运动员相对于水面的高度 h(单位:m)与起跳后的时间t(单位:s)存在函数关系 h(t)= -4.9t2+6.5t+10.如何用运动员在某些时间段内的平均速 度粗略地描述其运动状态?思考计算: 在这段时间里, =在这段时间里, =三、平均变化率概念:1.上述问题中的变化率可用式子表示, 称为函数 f(x)从x1到 x 2的平均变化率2.若设, (这里看作是对于 x1的一个“增量”可用 x1+代替 x2,同样)则平 均变...