山东省泰安市肥城市第三中学高中数学 导数的几何意义学案 新人教A版选修2-2

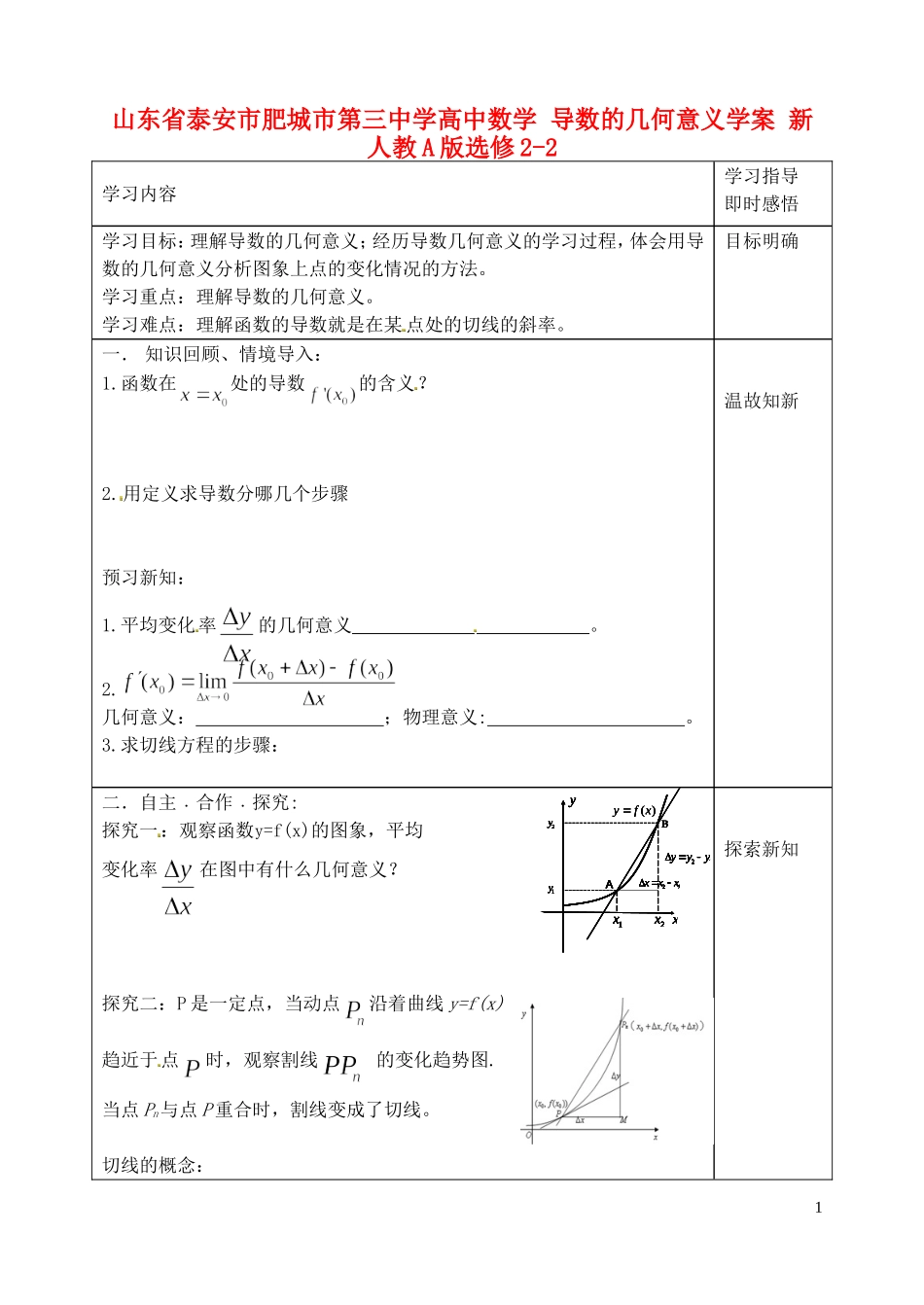
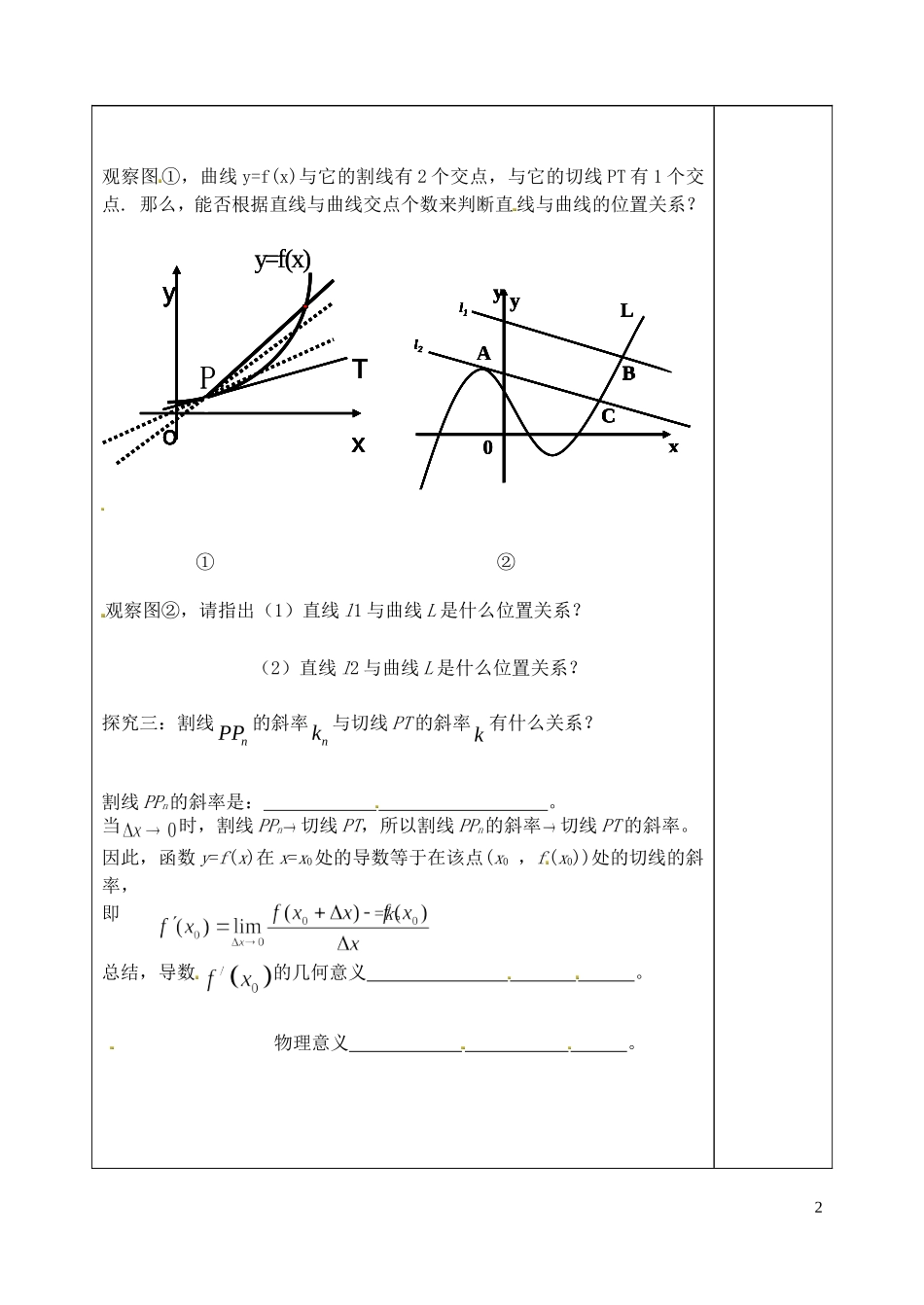
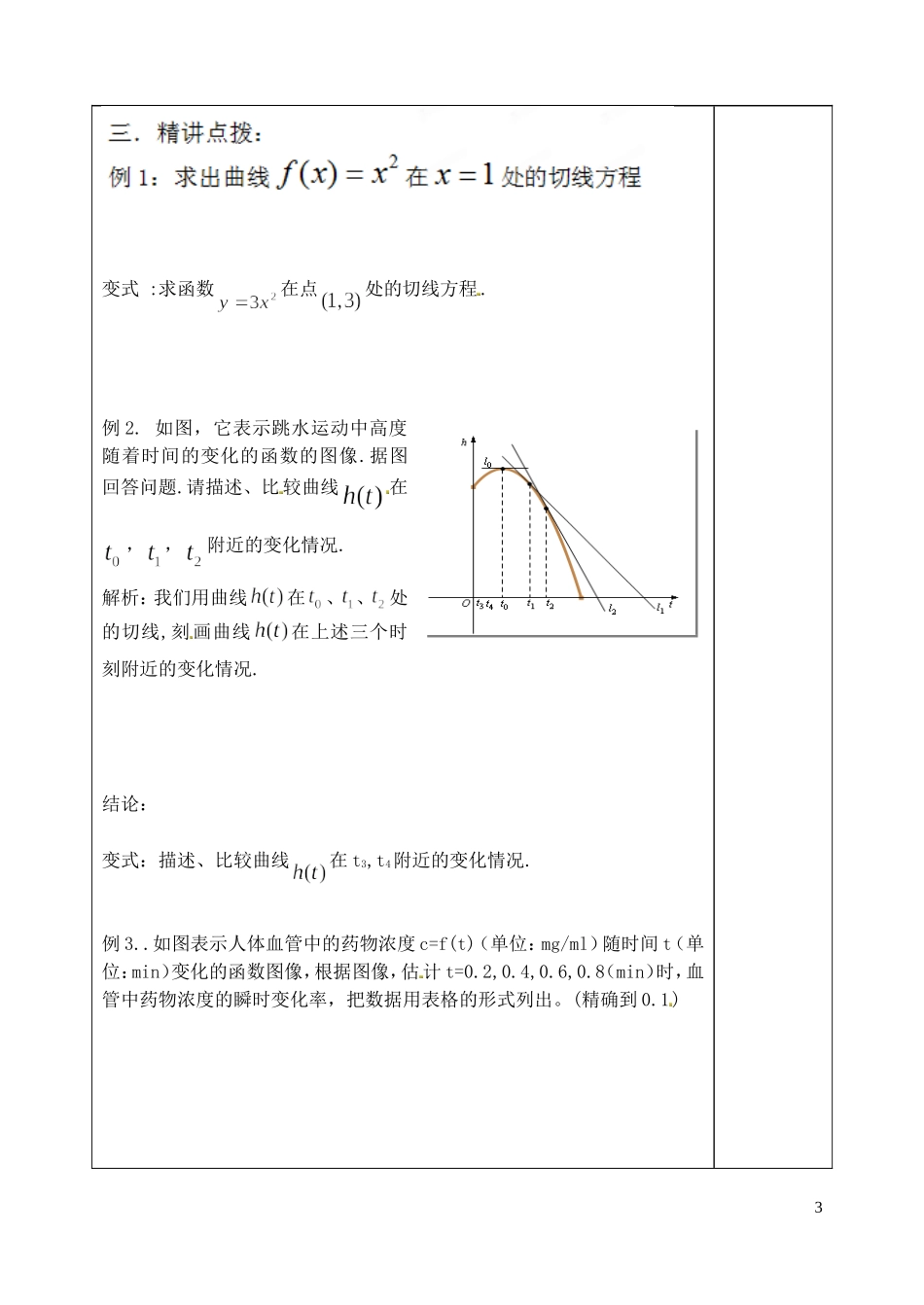
AB( )yf x21yyy 21xxx  2y1yyx2x1xAB( )yf x21yyy 21xxx  2y1yyx2x1xAB( )yf x21yyy 21xxx  2y1yyx2x1x( )yf x21yyy 21xxx  2y1yyx2x1x21yyy 21xxx  2y1yyx2x1x21yyy 21xxx  2y1yyx2x1x21yyy 21xxx  2y1yyx2x1x21yyy 21xxx  2y1yyx2x1x山东省泰安市肥城市第三中学高中数学 导数的几何意义学案 新人教 A 版选修 2-2学习内容学习指导即时感悟学习目标：理解导数的几何意义；经历导数几何意义的学习过程，体会用导数的几何意义分析图象上点的变化情况的方法。学习重点：理解导数的几何意义。学习难点：理解函数的导数就是在某 点处的切线的斜率。目标明确一． 知识回顾、情境导入：1.函数在处的导数的含义？2.用定义求导数分哪几个步骤预习新知：1.平均变化率的几何意义 。2.几何意义： ；物理意义: 。3.求切线方程的步骤：温故知新二．自主﹒合作﹒探究:探究一：观察函数y=f(x)的图象，平均变化率在图中有什么几何意义？ 探究二：P 是一定点，当动点沿着曲线 y=f(x)趋近于点时，观察割线 的变化趋势图.当点 Pn与点 P 重合时，割线变成了切线。切线的概念：探索新知1A0xyl2l1BxyCLA0A0xyl2l1BxyCLxyl2l1BxyCxyl2l1BxyCl2l1Bxyl2l1BxyCL观察图①，曲线 y=f(x)与它的割线有 2 个交点，与它的切线 PT 有 1 个交点. 那么，能否根据直线与曲线交点个数来判断直 线与曲线的位置关系？TxyoPy=f(x)TxyoTxyoTxyoxyoxyoxyoPy=f(x) ① ②观察图②，请指出（1）直线 l1 与曲线 L 是什么位置关系？（2）直线 l2 与曲线 L 是什么位置关系？探究三：割线nPP 的斜率nk 与切线 PT 的斜率k 有什么关系？ 割线 PPn的斜率是： 。当时，割线 PPn切线 PT，所以割线 PPn的斜率切线 PT 的斜率。因此，函数 y=f(x)在 x=x0处的导数等于在该点(x0 ，f(x0))处的切线的斜率，即 =k。总结，导数的几何意义 。 物理意义 。2变式 :求函数在点处的切线方程 .例 2. 如图，它表示跳水运动中高度随着时间的变化的函数的图像.据图回答问题.请描述、比 较曲线在，，附近的变化情况.解析：我们用曲线在、 、 处的切线,刻 画曲线在上述三个时刻附近的变化情况.结论：变式：描述、比较曲线在 t3,t4附近的变化情况.例 3..如图表示人体血管中的药物浓度 c=f(t)（单位：mg/ml）随...