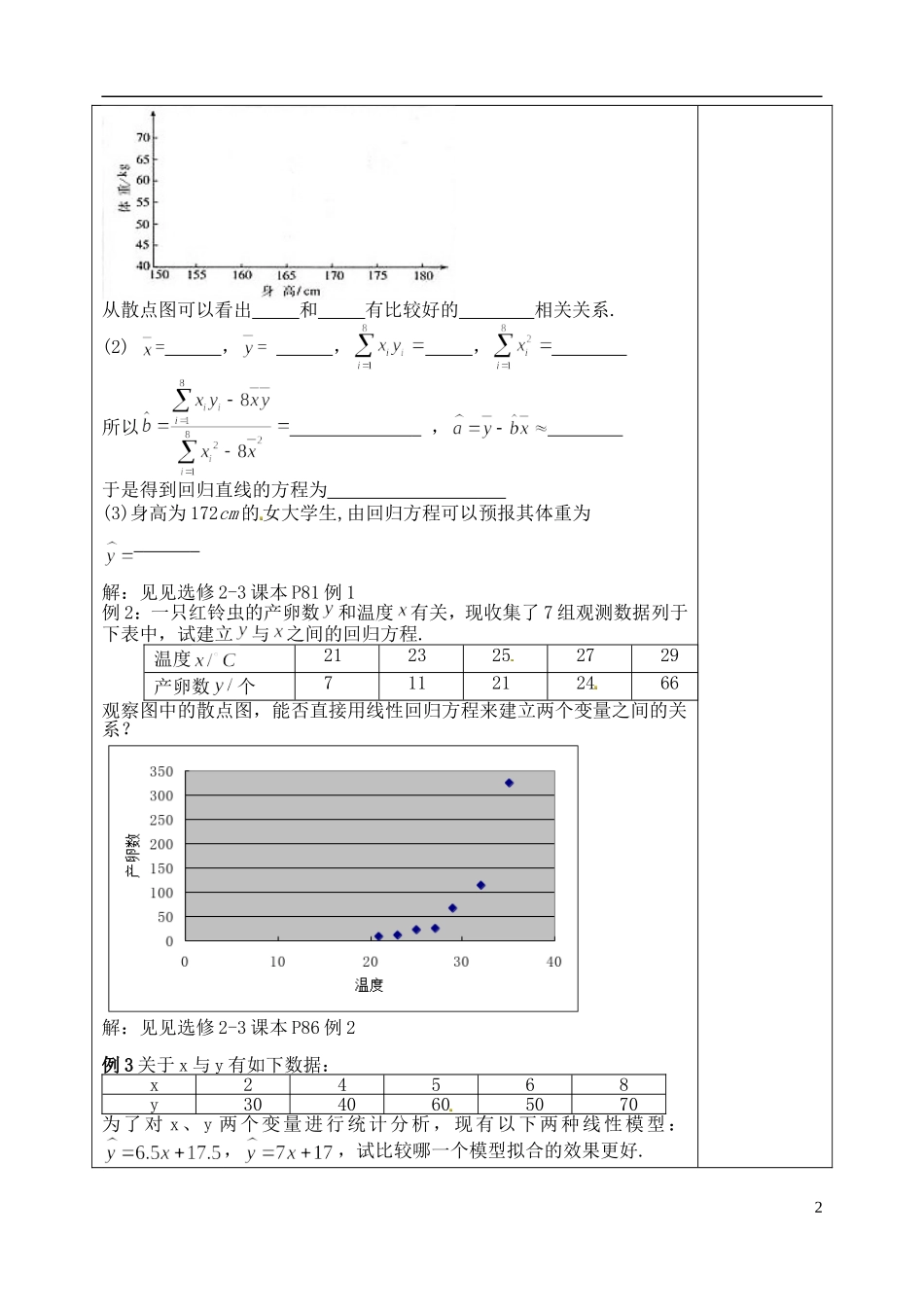
山东省泰安市肥城市第三中学高中数学 回归分析的基本思想及其初步应用学案 新人教 A 版选修 2-3学习内容学习指导即时感悟【学习目标】1、了解随机误差、残差等概念;2、掌握建立回归模型的步骤;3、通过典型案例的探究,进一步了解回归分析的基本思想、方法及初步应用。【学习重点】1、求回归直线方程,并且会利用回归直线方程进行估计;2、利用 R2表示拟合效果。【学习难点】利用 R2表示拟合效果。【回顾·复习】1、在回归直线方程中,如何求 ,解:见选修 2-3 课本 P802、回归直线方程一定通过哪个点?解:【自主·合作·探究】一般的,建立回归模型的基本步骤:(1)_________________________________ ______________________(2)_______________________________________________________(3)_______________________________________________________(4)_______________________________________________________(5)_______________________ _____________________________例 1、从某大学中随机选取 8名女大学生,其身高/cm 和体重/kg 数据如下表所示:编号123456 78身高16516515717017516 5155 170体重4857505464614359问题:画出散点图 ,求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为 172cm 的女大学生的体重.解:由于问题中要求根据身高预报体重,因此选 为自变量 x, 为因变量.(1)画散点图:1从散点图可以看出 和 有比较好的 相关关系.(2) = ,= , , 所以 , 于是得到回归直线的方程为 (3)身高为 172cm 的女大学生,由回归方程可以预报其体重为 解:见见选修 2-3 课本 P81 例 1例 2:一只红铃虫的产卵数和温度有关,现收集了 7 组观测数据列于下表中,试建立与之间的回归方程.温度 21 23 25 27 29产卵数个 7 11 21 24 66观察图中的散点图,能否直接用线性回归方程来建立两个变量之间的关系? 解:见见选修 2-3 课本 P86 例 2例 3 关于 x 与 y 有如下数据: x 2 4 5 6 8 y 30 40 60 50 70为了对 x、y 两个变量进行统计分析,现有以下两种线性模型:,,试比较哪一个模型拟合的效果更好.2解:第一个模型拟合效果好【当堂达标】1、下列两个变量具有相关关系的是( C )A. 正方体的体积与边长 B. 人的身高与视力C.人的身高与体重 D.匀速直线运动中的位移与时间2、已知回归直线方程,则时,y 的估计值为 11.69 3、观...