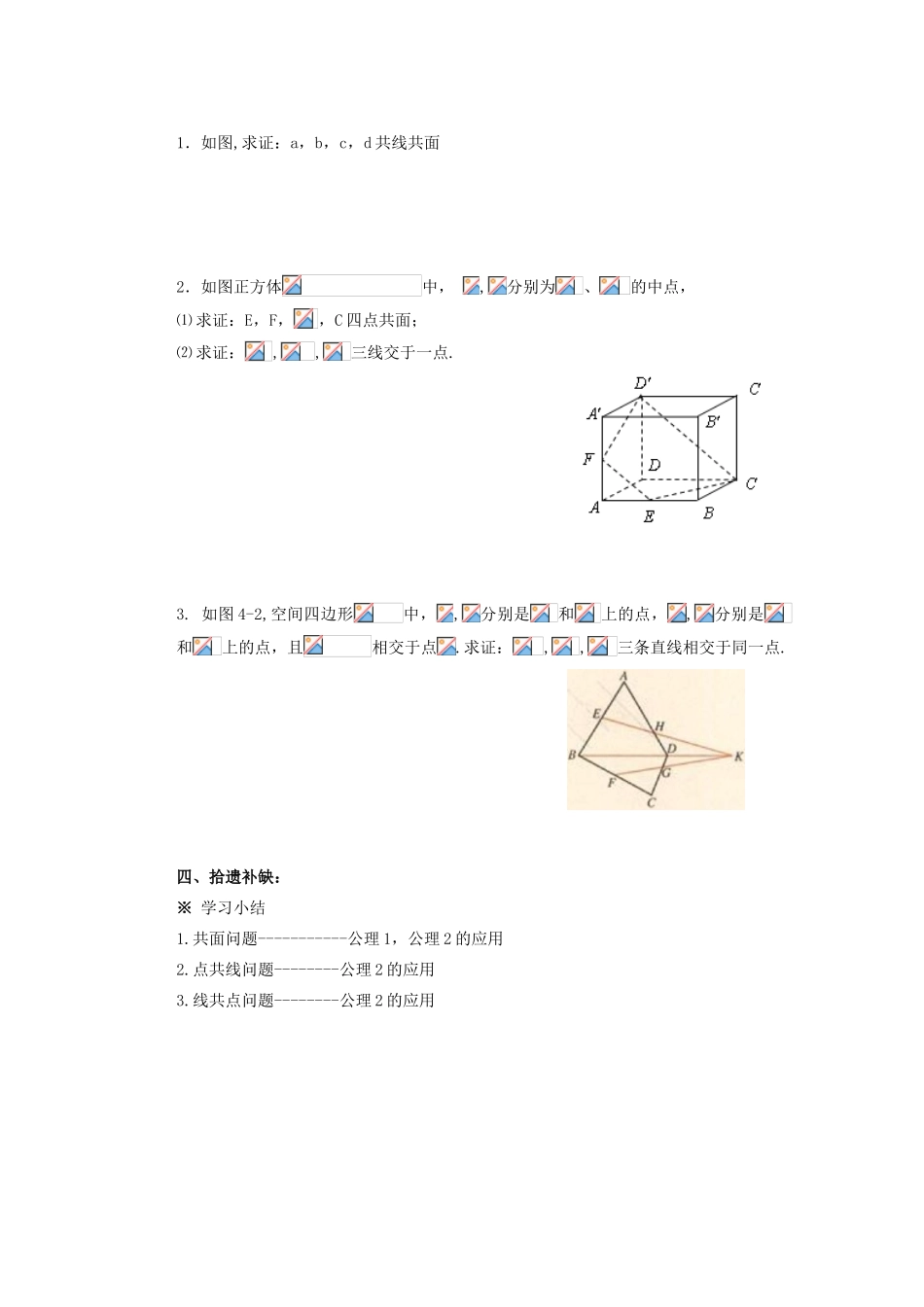
山西省朔州市平鲁区李林中学高中数学 平面(2)导学案 新人教 A 版必修 2一、课前导学:1.掌握平面的表示方法和基本画法;2.进一步掌握平面的基本性质;3.会应用公理 1,公理 2,公理 3 解决共点、共线、共面问题.二、课堂识真:1.复习回顾:复习 1:平面的特点是______、 _______ 、_______.复习 2:平面的基本性质(三个公理)公理 1___________________________________;公理 2___________________________________;公理 3___________________________________.巩固练习:① 如图,直线在内,判断是否在内;②“线段在平面内,直线不全在平面内”这一说法是否正确,为什么?③ 如果一条直线过平面内一点和平面外一点,那么它和这个平面有几个公共点?说明理由.2.讲授新课:一、共面问题证明若干个点、直线在同一个平面内方法一:平面纳入法------先确定一个平面,再证明其余的点、线在此平面内方法二:同一法------------根据已知点、线确定几个平面,再证明这几个平面重合(有且只有一个)方法三:反证法例 1:求证:三条两两相交但不共点直线共面.例 2:求证:如果两条平行线都和第三条直线相交,那么这三条直线共面。例 3:直线∥∥,,, 求证:四条直线共面.二、点共线问题------------三点共线方法一:找出两个平面,证明这些点都是两个平面的公共点,根据公理 3,这些点都在交线上,即证若干点共线方法二:选择其中两点确定一条直线,证明另外一些点也都在这条直线上.例 4: 已知:在平面外, 求证:三点共线. 三、三线共点问题方法:先证明两条直线交于一点,再证明第三条直线经过这点--------根据公理 3,把第三条直线作为前两条直线所在平面的交线例 5:正方体中,E,F 分别是 AB,BC 的中点,M,N 分别为的中点,求证:EF,DC,MN 三线交于一点三、课后见功:1.如图,求证:a,b,c,d 共线共面2.如图正方体中, ,分别为、的中点,⑴ 求证:E,F,,C 四点共面;⑵ 求证:,,三线交于一点.3. 如图 4-2,空间四边形中,,分别是和上的点,,分别是和上的点,且相交于点.求证:,,三条直线相交于同一点. 四、拾遗补缺:※ 学习小结1.共面问题-----------公理 1,公理 2 的应用2.点共线问题--------公理 2 的应用3.线共点问题--------公理 2 的应用