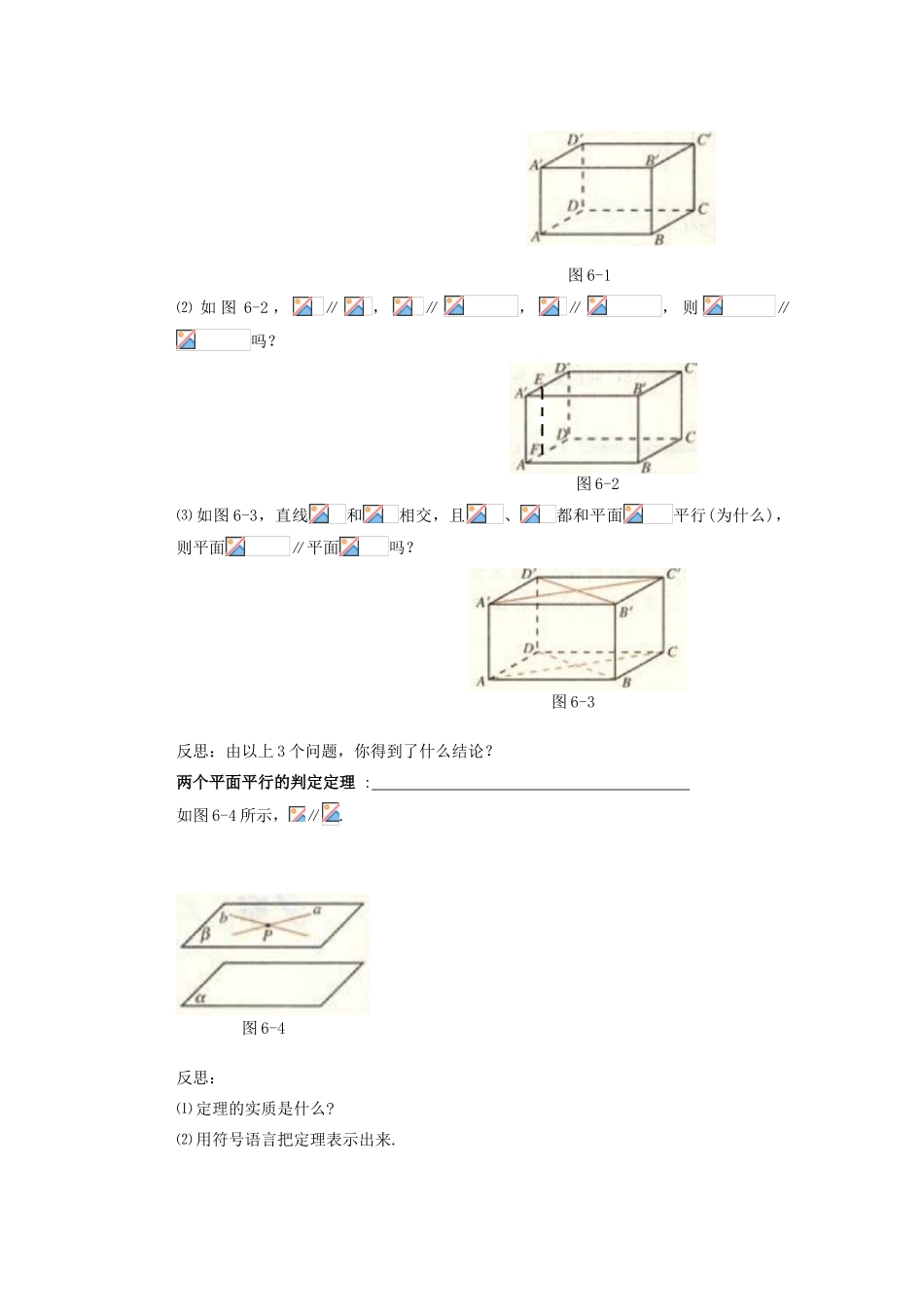
山西省朔州市平鲁区李林中学高中数学 平面与平面平行的判定导学案 新人教 A 版必修 2一、一、课前导学:学习目标 1. 能借助于长方体模型讨论直线与平面、平面与平面的平行问题;2. 理解和掌握两个平面平行的判定定理及其运用;3. 进一步体会转化的数学思想.二、课堂识真:1.导入新课:(预习教材 P56~ P57,找出疑惑之处)复习 1:直线与平面平行的判定定理是__________ _复习 2:两个平面的位置关系有___种,分别为_______和_______.讨论:两个平面平行的定义是两个平面没有公共点,怎样证明两个平面没有公共点呢?你觉得好证吗?2.讲授新课:探究:两个平面平行的判定定理问题 1:平面可以看作是由直线构成的,若一平面内的所有直线都与另一个平面平行,则这两个平面平行吗?由此你可以得到什么结论?结论:两个平面平行的问题可以转化为一个平面内的 与另一个平面平行的问题.问题 2:一个平面内所有直线都平行于另外一个平面好证明吗?能否只证明一个平面内若干条直线和另外一个平面平行,那么这两个平面就平行呢?问题 3:在长方体中,回答下列问题⑴ 如图 6-1,,∥面,则面∥面吗? 图 6-1⑵ 如 图 6-2 ,∥,∥,∥, 则∥吗? 图 6-2⑶ 如图 6-3,直线和相交,且、都和平面平行(为什么),则平面∥平面吗? 图 6-3反思:由以上 3 个问题,你得到了什么结论?两个平面平行的判定定理 : 如图 6-4 所示,∥. 图 6-4反思:⑴ 定理的实质是什么?⑵ 用符号语言把定理表示出来. ⑶ 如果要证明定理,该怎么证明呢?问题:你能总结出证明面面平行有哪几种方法吗?3.典型例题例 1.下列说法中正确的是( ) A.若平面内无数条直线分别与平面平行,则 B.两个平面分别经过两条平行线,则这两个平面平行 C.过已知平面外一条直线,必能作出与已知平面平行的平面 D.一个平面内有两条相交的直线都与另一平面平行,则这两个平面平行例 2. 已知正方体,如图 6-5,求证:平面∥. 图 6-5例 3. 如图 6-6,、、分别是、、的重心.求证:面∥. 图 6-6 小结:证明面面平行,只需证明线线平行,而且这两条直线必须是相交直线.三、课后见功:1. 平面与平面平行的条件可以是( ). A.内有无穷多条直线都与平行 B.直线与都平行,且不在和内 C.直线,直线,且∥,∥ D.内的任何直线都与平行2. 经过平面外的一条直线且与平面平行的平面( ). A.有且只有一个 B.不存在 C.至多有一个 D.至少有一个3. 设有...