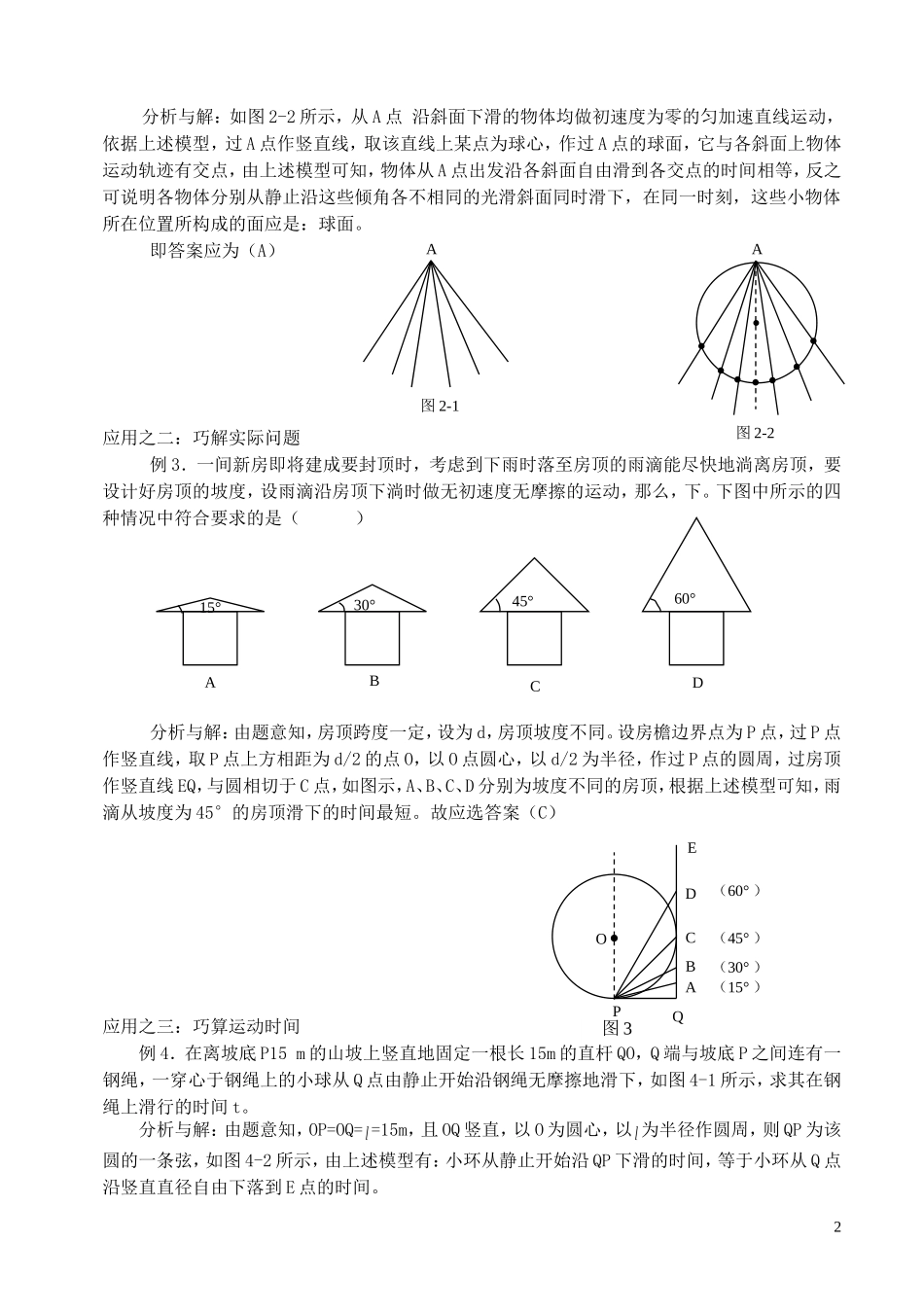
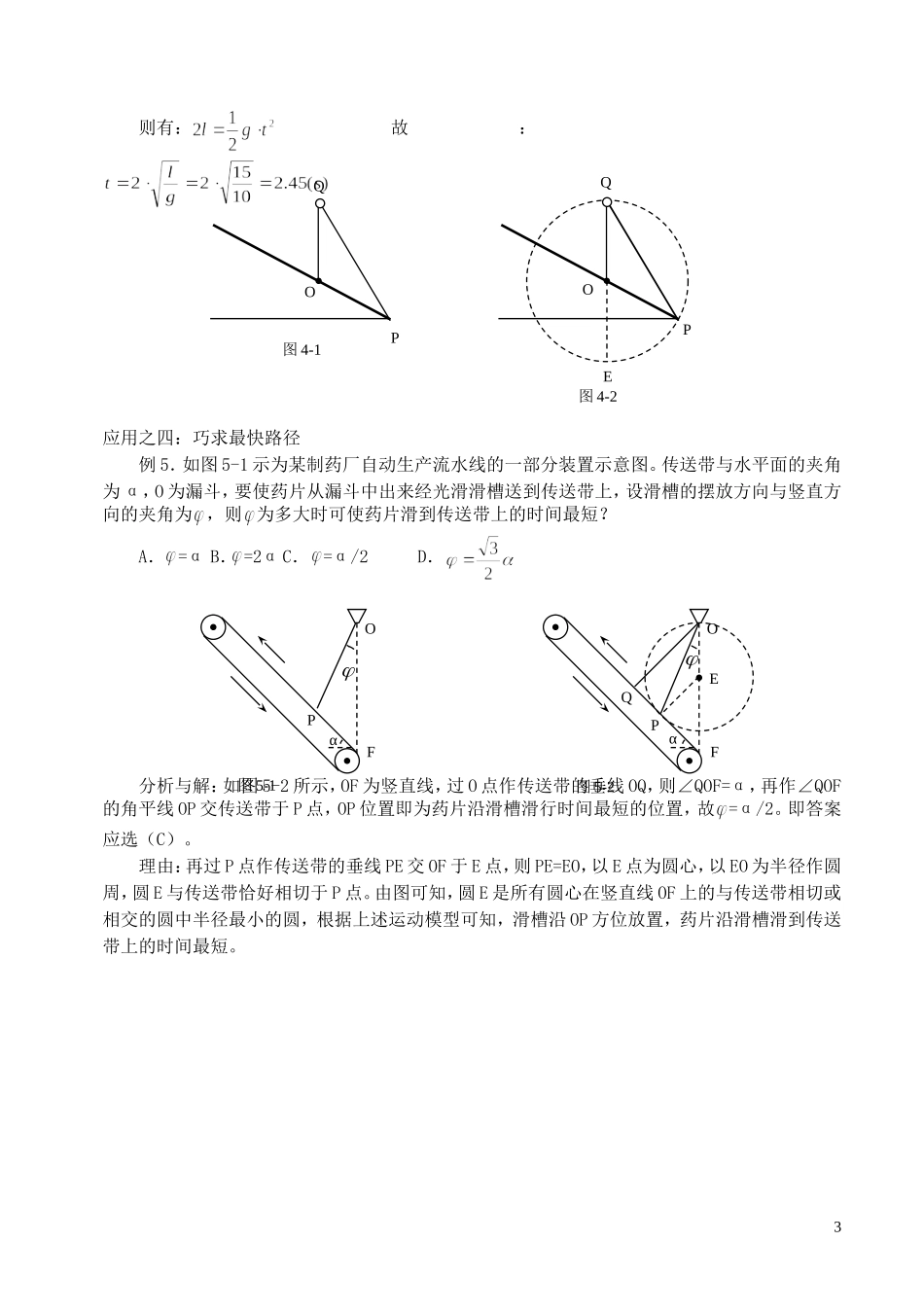
巧用运动模型 速解物理问题 单柏荣(湖南省衡东县第二中学13787713501)运动模型:如图所示,竖直放置的半径为 R 的圆环,PQ 为该圆环竖直直径,试证明:物体从P 点沿任意光滑直杆自由滑到圆环上各点的时间相等,且等于沿竖直直径自由下滑的时间:。证明:如图所示,PA、PB、PC、PD 为竖直圆环上过 P 点的任意弦,设任意弦 PA 与直径 PQ 夹角为 θ,则物体沿光滑直杆 PA 下滑的加速度 a=gcosθ,PA 长为 2Rcosθ,物体沿 PA 作初速度为零的匀加速直线运动到达 A 点的时间为 t,则有:故有:(与 θ 角无关)由上述分析可知,前面的结论成立。应用之一:巧做选择题。例 1、如图所示,AC、BC 为位于竖直平面内的两根光滑细杆,A、B、C 三点恰位于同一个圆周上,C 为该圆周的最低点,a、b 为套在细杆上的两个小环上,当两环同时从 A、B 点自静止开始下滑,则A、环 a 将先到达点 C B、环 b 将先到达点 C C、环 a, b 将同时到达点 C D、由于两杆的倾角不知道,无法判断 分析与解:如图 2 所示,过竖直直径的上端点分别作 AC、BC 的平行线、。由上述模型可知:由对称性可知,,故有:,答案为(C)例 2、如图 2-1 所示,通过空间任意一点 A,可作无限多个斜面,如果将若干个小球在 A 点分别从静止沿这些倾角各不相同的光滑斜面同时滑下,那么在同一时刻,这些小物体所在位置所构成的面是( )A、球面 B、抛物面C、水平面D、无法确定1abABbC图 1-1abABbC图 1-2C′B′A′BAQCDPθ分析与解:如图 2-2 所示,从 A 点 沿斜面下滑的物体均做初速度为零的匀加速直线运动,依据上述模型,过 A 点作竖直线,取该直线上某点为球心,作过 A 点的球面,它与各斜面上物体运动轨迹有交点,由上述模型可知,物体从 A 点出发沿各斜面自由滑到各交点的时间相等,反之可说明各物体分别从静止沿这些倾角各不相同的光滑斜面同时滑下,在同一时刻,这些小物体所在位置所构成的面应是:球面。即答案应为(A)应用之二:巧解实际问题例 3.一间新房即将建成要封顶时,考虑到下雨时落至房顶的雨滴能尽快地淌离房顶,要设计好房顶的坡度,设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么,下。下图中所示的四种情况中符合要求的是()分析与解:由题意知,房顶跨度一定,设为 d,房顶坡度不同。设房檐边界点为 P 点,过 P 点作竖直线,取 P 点上方相距为 d/2 的点 O,以 O 点圆心,以 d/2 ...