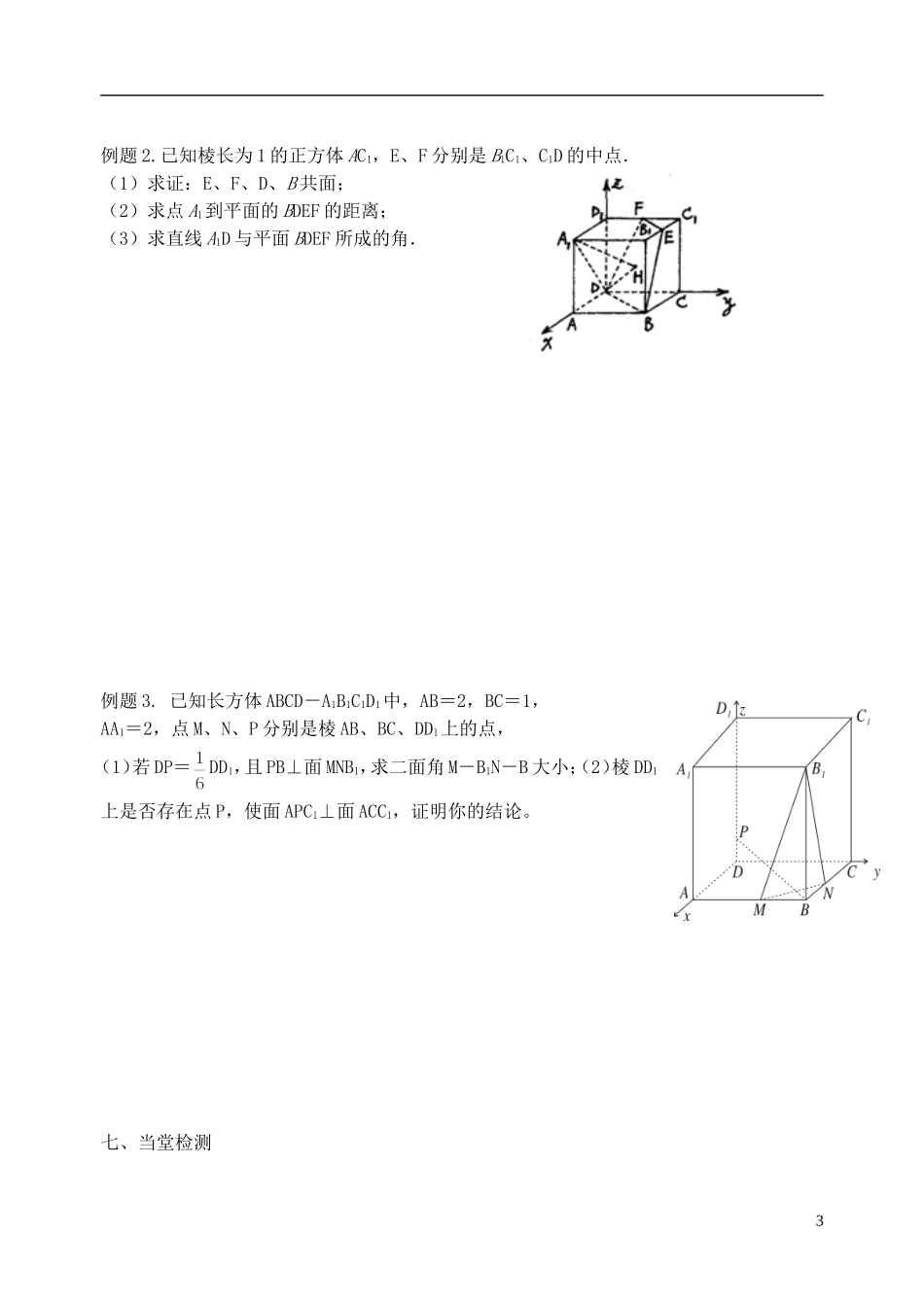
§2 利用空间向量求空间角、空间距离 1一、考纲要求内容要求空间向量与立体几何B二、教学目标1.会用向量法解决平行与垂直问题;2.掌握平面的法向量的求法;3.掌握向量法求空间角;4.会用向量法求点面距。三、重点难点:向量法求空间角四、知识导学1.若,则(1) (b1b2b3≠0)(2) (3) 2.设 A(x1,y1,z1) B(x2,y2,z2)则3.直线的方向向量.平面的法向量的概念及求法4.向量法解决几何问题的步骤:(1)建立空间直角坐标系,把立体几何问题转化为向量问题;(2)进行空间向量的运算,研究点、直线、平面之间的位置关系以及它们之间的夹角和距离问题;(3)把向量的运算结果“翻译”成相应的几何意义。五、课前自学1.在四棱锥 P-ABCD 中,PD⊥平面 ABCD,PA 与平面 ABCD 所成角是 600,底面 ABCD 中, ∠D=∠DAB=900, AB=4,CD=1,AD=2, 则异面直线 PA,BC 所成角的余弦值 .2.在正方体 ABCD-A1B1C1D1 中,F 是 BC 的中点,点 E1 在 C1D1 上,且则直线 E1F 和平面 D1AC 所成角的大小为 13. 四 棱 锥 P-ABCD 的 底 面 是 边 长 为 a 的 正 方 形 , PA⊥ 底 面 ABCD,E 是 PC 上 的 点 , 且CE:EP=1:2,(1)在线段 AB 上是否存在点 F,使得 EF∥平面 PAD?(2)若二面角 B-PC-D 的大小是 1200,求 PA 的长. 六、合作、探究、展示例题 1.已知正方体 ABCD-A1B1C1D1的棱长为 2,点 E 为棱 AB 的中点,求:(Ⅰ)D1E 与平面 BC1D 所成角的大小;(Ⅱ)二面角 D-BC1-C 的大小;(Ⅲ)异面直线 B1D1与 BC1之间的距离.2ABCD1A1B1C1DE例题 2.已知棱长为 1 的正方体 AC1,E、F 分别是 B1C1、C1D 的中点.(1)求证:E、F、D、B 共面;(2)求点 A1到平面的 BDEF 的距离;(3)求直线 A1D 与平面 BDEF 所成的角.例题 3. 已知长方体 ABCD-A1B1C1D1中,AB=2,BC=1,AA1=2,点 M、N、P 分别是棱 AB、BC、DD1上的点,(1)若 DP=DD1,且 PB⊥面 MNB1,求二面角 M-B1N-B 大小;(2)棱 DD1上是否存在点 P,使面 APC1⊥面 ACC1,证明你的结论。七、当堂检测31.已知长方体直线与平面所成的角为,垂直于,为的中点.(Ⅰ)求异面直线与所成的角;(II)求平面与平面所成的二面角;(III)求点到平面的距离.2.如图,在正四棱柱中,已知,、分别为、上的点,且(Ⅰ)求证:平面;(Ⅱ)求点到平面的距离.八、总结反思4EFADCD1A1C1B1B图9ABCDFE1A1B1C1D