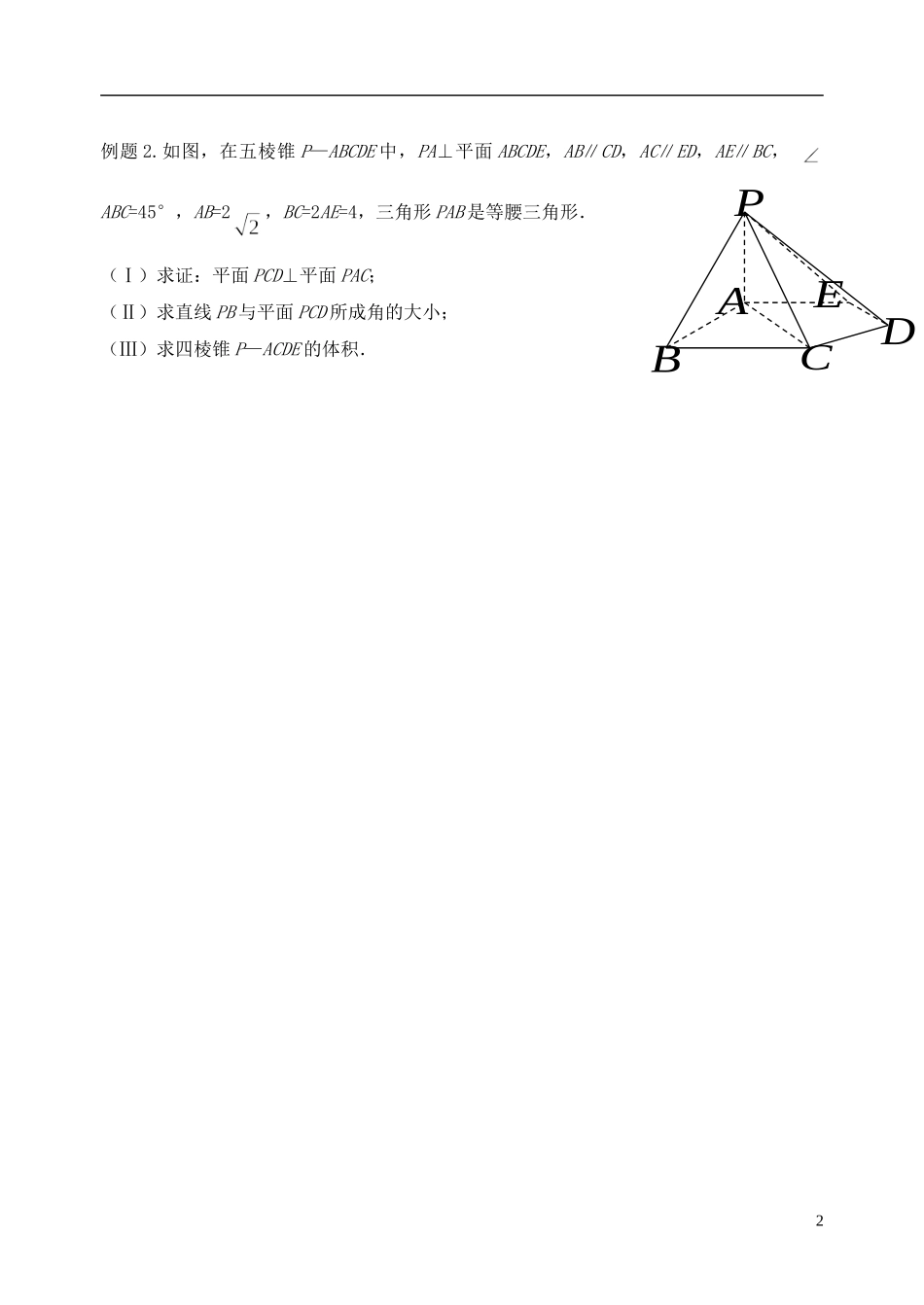
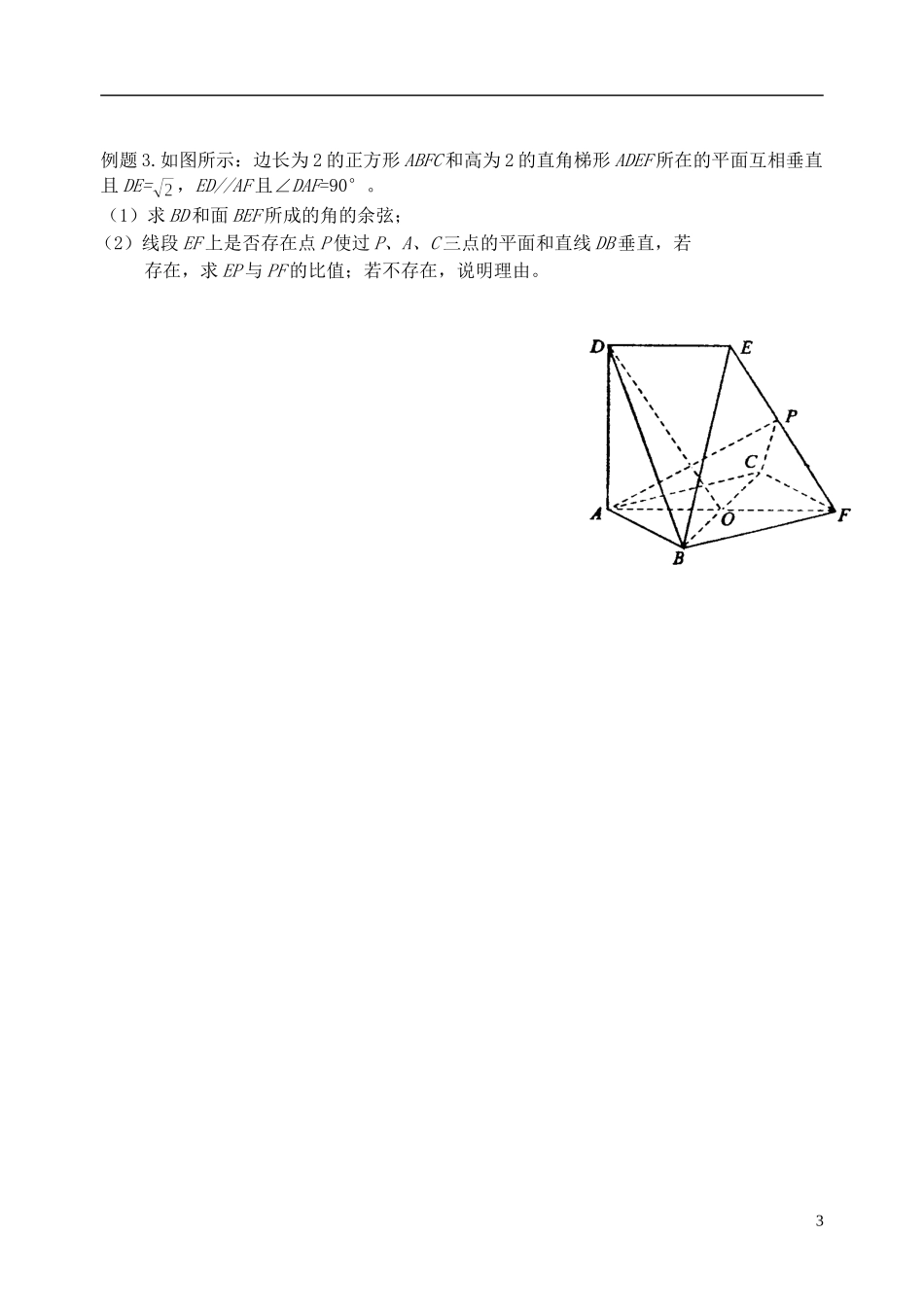
§3 利用空间向量求空间角与空间距离 2一、考纲要求内容要求空间向量综合应用B二、知识导学1. 向量法解决几何问题的步骤:(1)建立空间直角坐标系,把立体几何问题转化为向量问题。(2).进行空间向量的运算,研究点、直线、平面之间的位置关系以及它们之间的夹角和距离问题。(3).把向量的运算结果“翻译”成相应的几何意义。三、合作、探究、展示例 1.如图,四边形是直角梯形,∠=90°,∥,=1,=2,又=1,∠=120°,⊥,直线与直线所成的角为 60°.( Ⅰ ) 求 证 : 平 面⊥ 平 面; ( Ⅱ ) 求 二 面 角的 大 小 ;1例题 2.如图,在五棱锥 P—ABCDE 中,PA⊥平面 ABCDE,AB∥CD,AC∥ED,AE∥BC, ABC=45°,AB=2,BC=2AE=4,三角形 PAB 是等腰三角形.(Ⅰ)求证:平面 PCD⊥平面 PAC;(Ⅱ)求直线 PB 与平面 PCD 所成角的大小;(Ⅲ)求四棱锥 P—ACDE 的体积.2EDCBPA例题 3.如图所示:边长为 2 的正方形 ABFC 和高为 2 的直角梯形 ADEF 所在的平面互相垂直且 DE=,ED//AF 且∠DAF=90°。 (1)求 BD 和面 BEF 所成的角的余弦;(2)线段 EF 上是否存在点 P 使过 P、A、C 三点的平面和直线 DB 垂直,若存在,求 EP 与 PF 的比值;若不存在,说明理由。 3ADBCVxyz 四、当堂检测1.如图,在三棱锥 V-ABC 中,VC⊥底面 ABC,AC⊥BC,D 是 AB 的中点,且 AC =BC = a ,∠VDC=θ。(Ⅰ)求证:平面 VAB⊥平面 VCD ;(Ⅱ)当角 θ 变化时,求直线 BC 与平面 VAB 所成的角的取值范围; 2.如图,在直三棱柱中,分别是的中点,点在上,求证:(1)∥(2) 4五、总结反思5