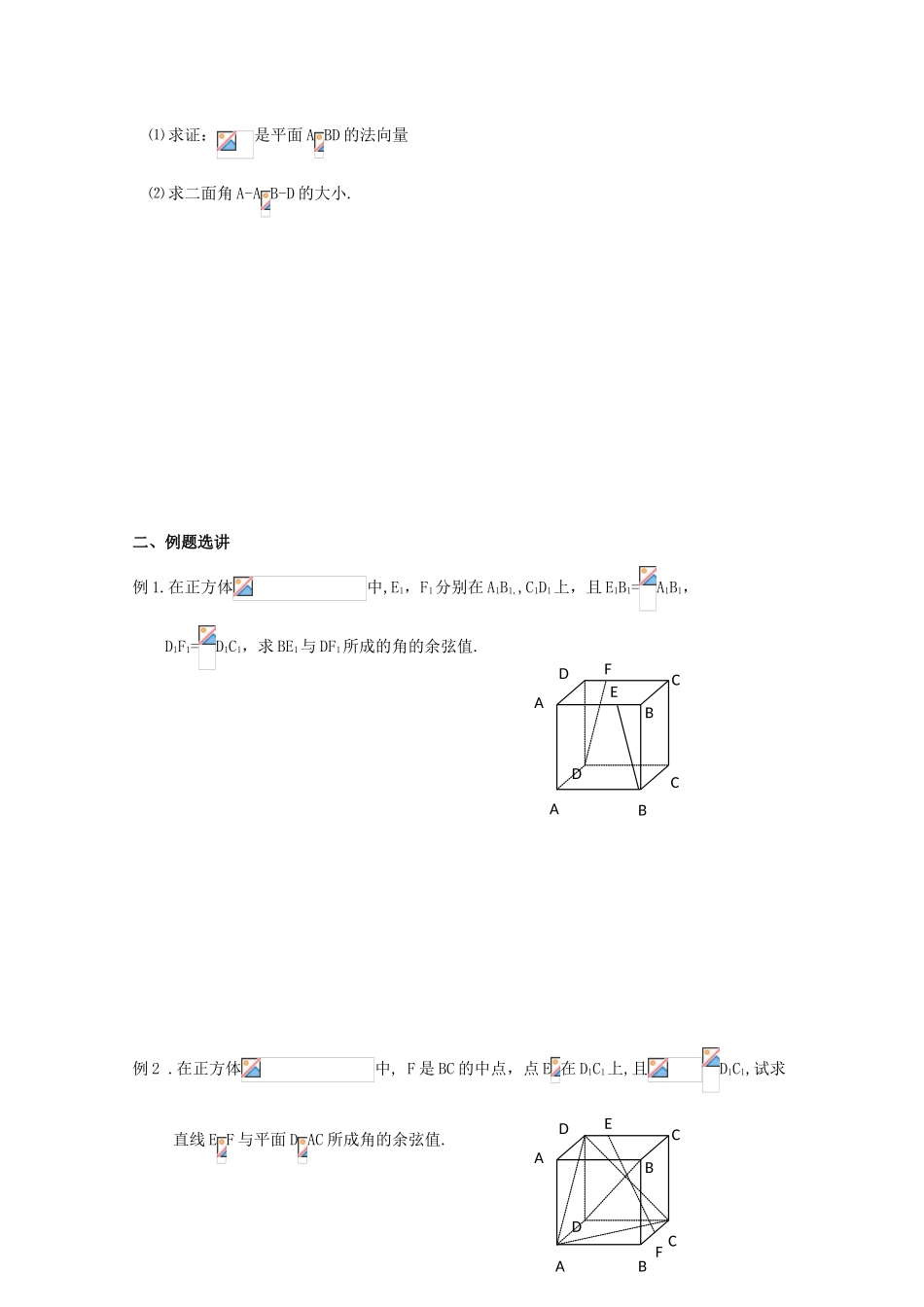
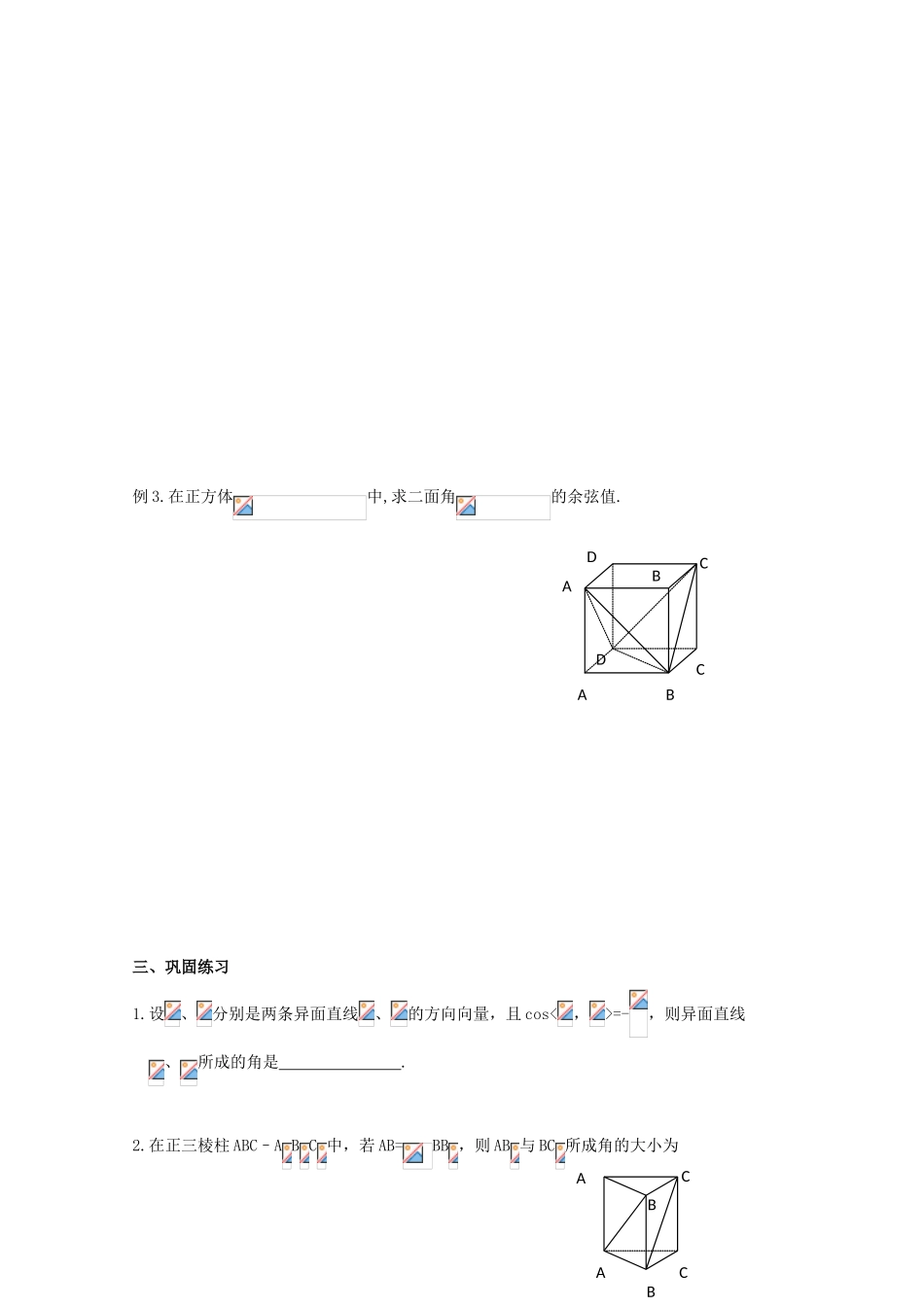
3.2.3 空间的角的计算【学习目标】能用向量方法解决线线、线面、面面角的计算问题【学习重点】异线角、线面角、二面角的计算一、课前预习1.两条异面直线所成的角的范围是 ,若两条异面直线所成的角为 θ, 它们的方向向量的夹角为,则 θ 与的关系是 .2.直线与平面所成的角的范围是 ,若直线与平面所成的角为 θ,直线的方向向量与平面的法向量的夹角为,则 θ 与的关系是 .3.二面角的平面角的范围是 ,二面角的平面角的大小为 θ,两个半平面的法向量所成的角为,则 θ 与的关系是 .4.在棱长为 1 的正方体 ABCD–A B C D 中,M、N 分别是 A B 、BB 的中点,求直线 AM 与 CN 所成的角的余弦值.5.正方体 ABCD–A B C D 中,求直线 BC 与平面 A BD 所成的角的余弦值.6.如图,在正方体 AC 中,O 是底面 ABCD 的中心,M 是 CC 的中点.ABCDABCDMNABCDABCDABCDABCDOM ⑴ 求证:是平面 A BD 的法向量 ⑵ 求二面角 A-A B-D 的大小.二、例题选讲例 1.在正方体中,E1,F1分别在 A1B1,,C1D1上,且 E1B1=A1B1,D1F1=D1C1,求 BE1与 DF1所成的角的余弦值.例 2 .在正方体中, F 是 BC 的中点,点 E 在 D1C1上,且D1C1,试求直线 E F 与平面 D AC 所成角的余弦值.ABCDABCDEFABCDABCDFE例 3.在正方体中,求二面角的余弦值.三、巩固练习1.设、分别是两条异面直线、的方向向量,且 cos<,>=-,则异面直线 、所成的角是 .2.在正三棱柱 ABC–A B C 中,若 AB=BB ,则 AB 与 BC 所成角的大小为ABCABCABCDABCD .3.已知正方体 ABCD–A B C D 中,M 是 AB 的中点,则对角线 DB 与 CM 所成的角的余弦值是 .4.在正方体 ABCD–A B C D 中,点 E 为 BB 的中点,求平面 A ED 与平面 ABCD 所成的 锐二面角的余弦值.ABCDABCDMABCDABCDE