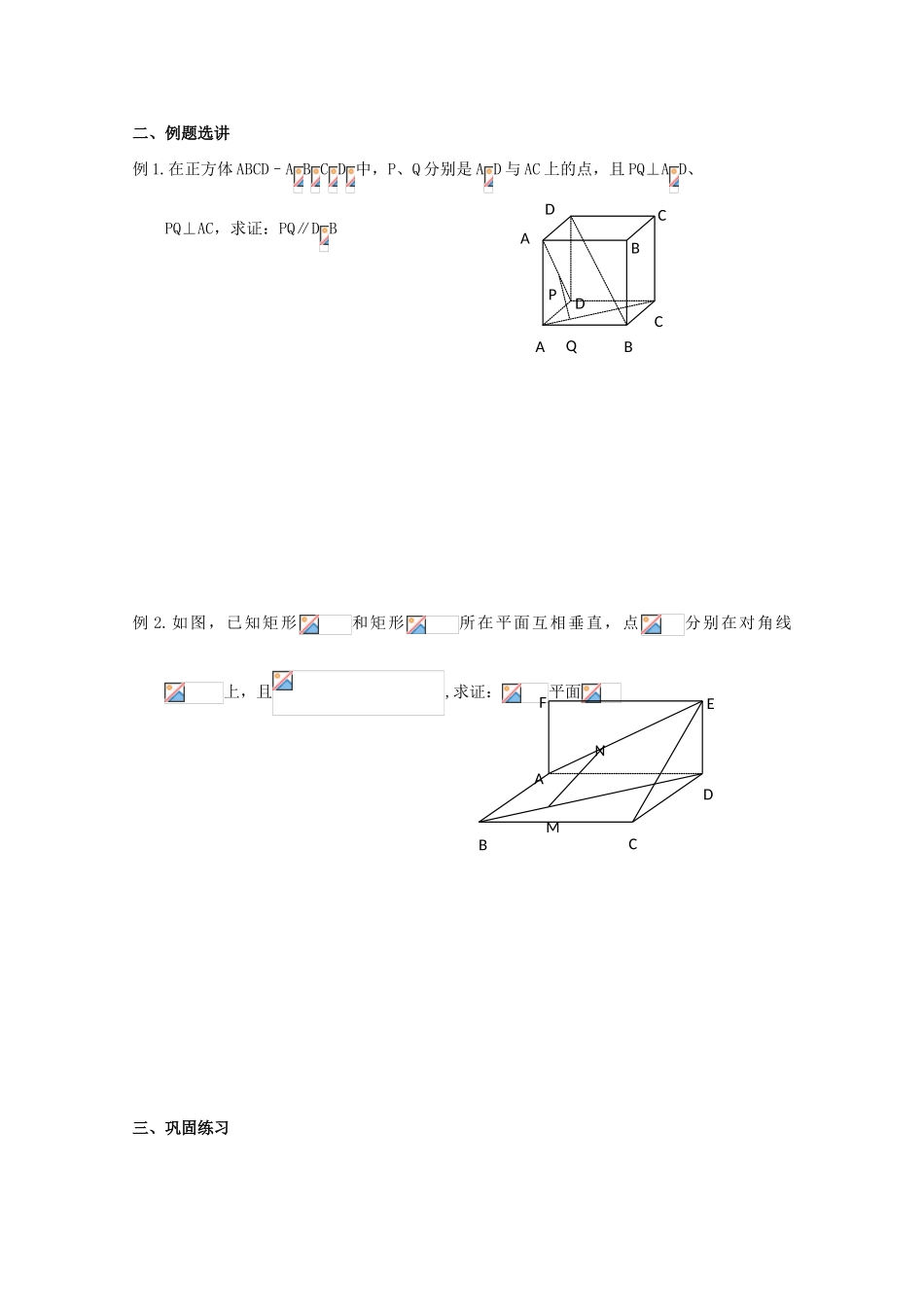
3.2.2 空间线面关系的判定(二)【学习目标】1.能用向量语言描述线线、线面、面面的平行关系2.能用向量方法判断空间线面的平行关系【学习重点】用向量方法判断空间线面的平行关系一、课前预习1.若直线、的方向向量分别为、,平面 α、β 的法向量分别为、,则 ⑴∥ , ⑵∥α , ⑶α∥β .2.若=(2x,1,3),=(1,-2y,9),若、为共线向量,则 x= , y= .3.已知 A(2,-1,2)、B(4,5,-1)、C(-2,2,3),且=,则 P 点的坐标 是 .4.已知 A(1,2,3)、B(2,1,2)、P(1,1,2),点 Q 在直线 OP 上运动,则当 •取最小值时,求点 Q 的坐标二、例题选讲例 1.在正方体 ABCD–A B C D 中,P、Q 分别是 A D 与 AC 上的点,且 PQ⊥A D、 PQ⊥AC,求证:PQ∥D B例 2.如图,已知矩形和矩形所在平面互相垂直,点分别在对角线上,且,求证:平面三、巩固练习ABCDEFMNABCDABCDPQ1.已知=(1,2,-2),若∣∣=2∣∣,且∥,则= .2.向量与=(2,-1,2)共线,且满足•=18,( k+)⊥(k–), 则= ,k= .3.在长方体 OAEB-O A E B 中,OA=3,OB=4,OO =2,点 P 在棱 AA 上,且 AP=2PA , 点 S 在棱 BB 上,且 SB =2BS,点 Q、R 分别是 O B 、AE 的中点,求证:PQ∥RS4.在正方体 ABCD–A B C D 中,M、N 分别是 CC 、B C 的中点,求证:MN∥面 A BDOAEBOAEBPQSRABCDABCDNM