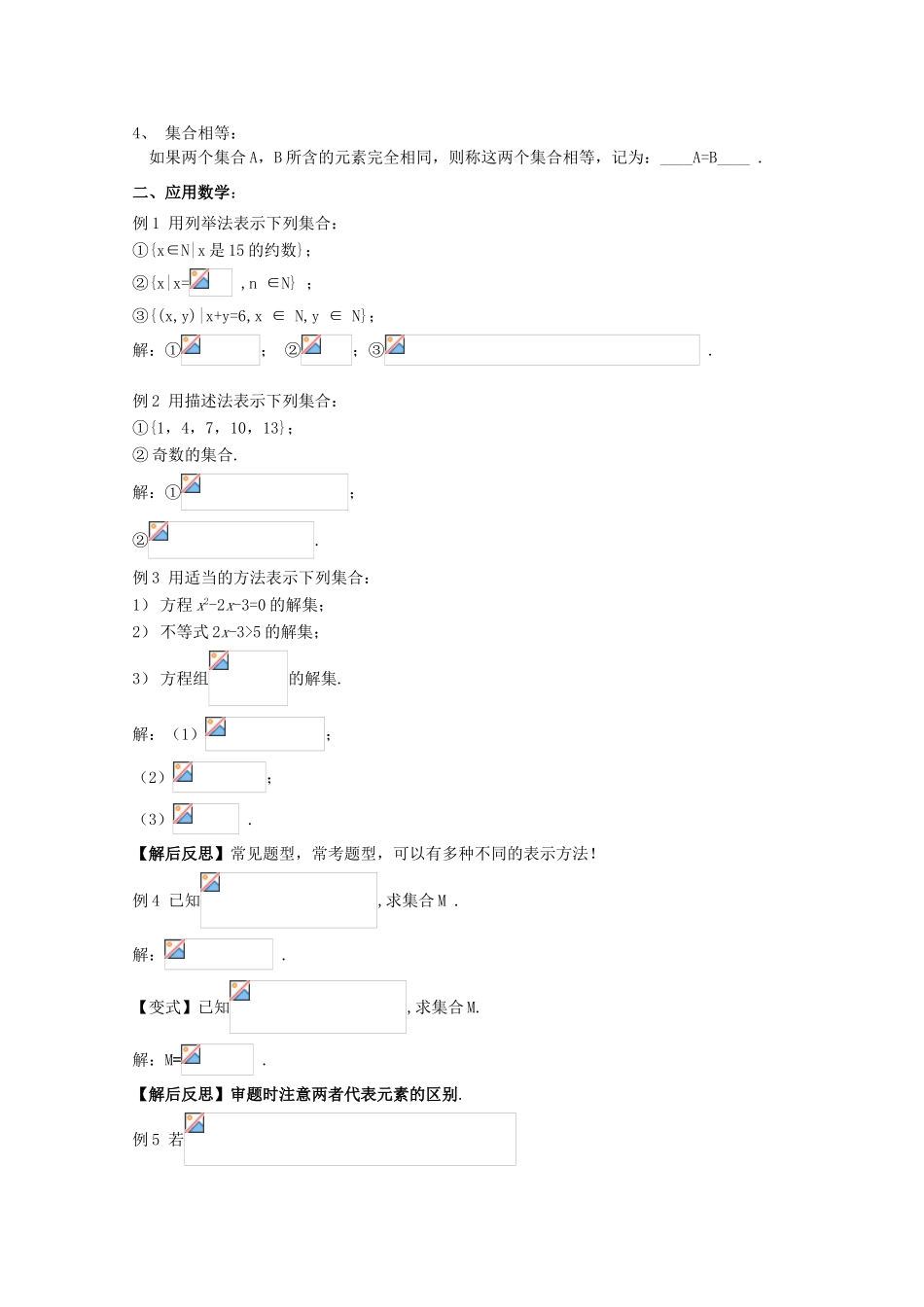
第 2 课时 集合的含义及其表示(二)【学习目标】1.理解并掌握集合三种表示方法;熟练地进行集合表示方法之间的转换;2.初步理解集合相等的概念,并会初步运用;3.培养学生的逻辑思维能力和运算能力.【课前导学】一、复习回顾:1、 集合的概念描述:1)一般地,一定范围内某些 确定的、不同的对象的全体 构成一个集合。2)集合的元素具有__确定____性、_互异__性和__无序__性.3)如果 a 是集合 A 的元素,记作________.4)集合的分类: 有限集,无限集和空集 .2、 常用数集的符号:自然数集__N____;正整数集__N*____;整数集__Z____;有理数集__Q____;实数集__R___.二、思考题:集合 A 中的元素由 x=a+b(a∈Z,b∈Z)组成,判断下列元素与集合 A 的关系? (1)0 (2) (3)分析:先把 x 写成 a+b的形式,再观察 a,b 是否为整数.【解】(1)因为,所以;(2)因为,所以;(3)因为, 所以 .点评: 要判断某个元素是否是某个集合的元素,就是看这个元素是否满足该集合的特性或具体表达形式. 三、问题情境观察下列对象能否构成集合(1)满足 x-3>2 的全体实数;(2)本班的全体男生;(3)我国的四大发明;(4)2008 年北京奥运会中的球类项目;(5)不等式 2x+3 < 9 的自然数解;(6)所有的直角三角形; 如果能够,那么这些集合又如何来表示?【课堂活动】一、建构数学:1、列举法:将集合的元素一一列举出来,并置于花括号“{ }”内.用这种方法表示集合,元素要用逗号隔开,但与元素的次序无关.思考:用列举法表示下列对象构成集合:(6)所有的直角三角形.【提醒】 (1)如果两个集合所含元素完全相同( 即 A 中的元素都是 B 中的元素,B 中的元素也都是 A中的元素),则称这两个集合相等.(2)a 与{a}不同:a 表示一个元素,{a}表示一个集合,该集合只有一个元素.(3)集合{(1,2),(3,4)}与集合{1,2,3,4}不同 .2、描述法:将集合的所有元素都具有的性质(满足的条件)表示出来,写成{x|p(x)}的形式.如:{x|x 为中国直辖市},{x|x 为 young 中的字母} .所有直角三角形的集合可以表示为: { x|x 是直角三角形}等.3、Venn 图法: 用封闭的曲线内部表示集合(形象直观).如:集合{x|x 为 young 中的字母}.【思考】何时用列举法?何时用描述法?(1)有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法.如 :集合{ 3,7,8 }.(2)有些集合的元...