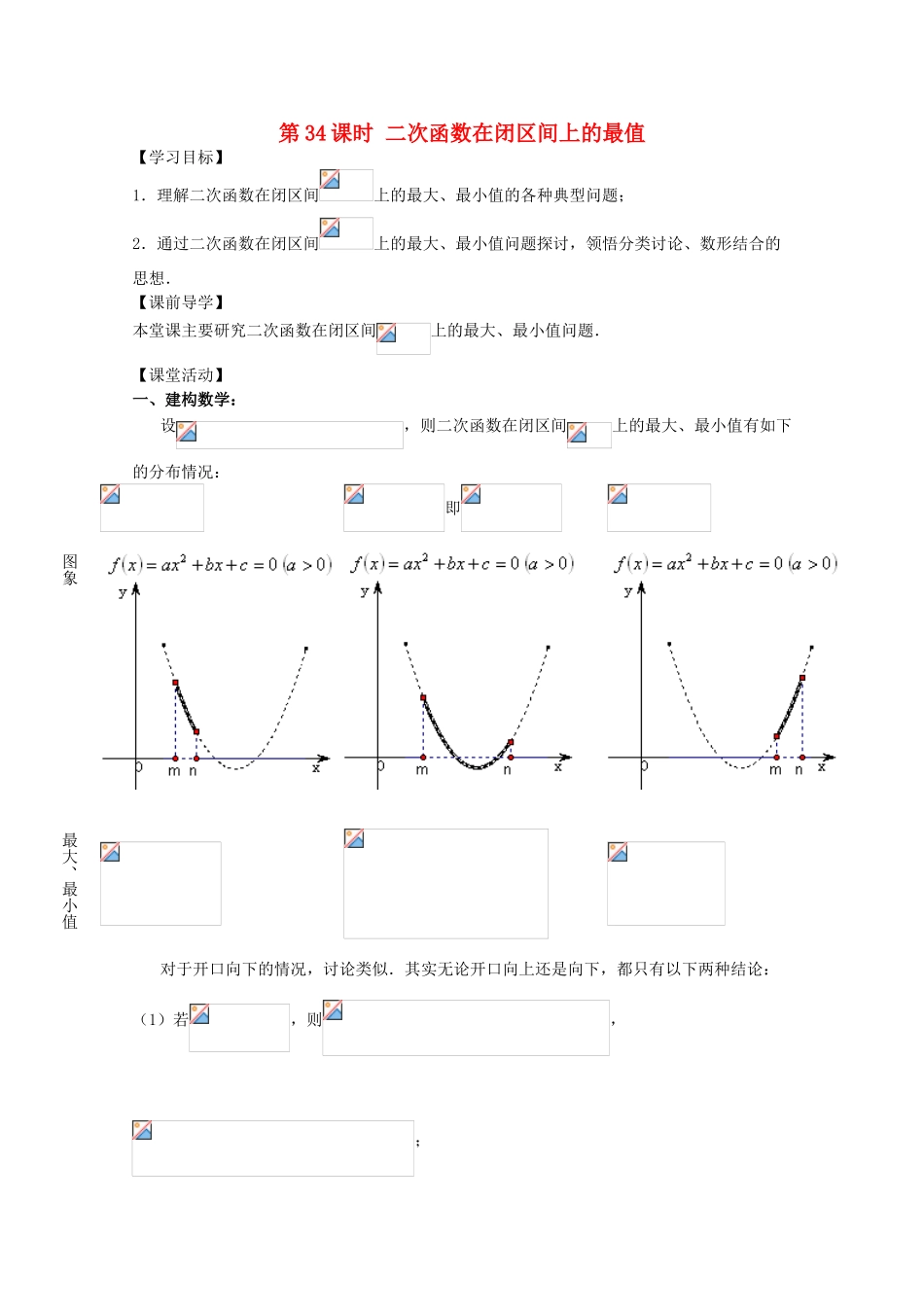
第 34 课时 二次函数在闭区间上的最值【学习目标】1.理解二次函数在闭区间上的最大、最小值的各种典型问题;2.通过二次函数在闭区间上的最大、最小值问题探讨,领悟分类讨论、数形结合的思想.【课前导学】本堂课主要研究二次函数在闭区间上的最大、最小值问题.【课堂活动】一、建构数学:设,则二次函数在闭区间上的最大、最小值有如下的分布情况:即图象最大、最小值对于开口向下的情况,讨论类似.其实无论开口向上还是向下,都只有以下两种结论:(1)若,则,;(2)若,则,另外,当二次函数开口向上时,自变量的取值离开对称轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开对称轴轴越远,则对应的函数值越小.二、应用数学:例 1 函数在上有最大值 5 和最小值 2,求的值.【分析】注意开口方向的讨论.解:对称轴,故函数在区间上单调.(1)当时,函数在区间上是增函数,故 ;(2)当时,函数在区间上是减函数,故 .【解后反思】处理二次函数最值问题首先要关注开口方向的讨论.例 2 求函数的最小值.【分析】动轴定区间,按对称轴与定义域区间的位置关系,由数形结合可得在上的最大值或最小值.解:对称轴(1)当时,;(2)当时,;(3)当时,.【变式】1、本题若修改为求函数的最大值,过程又如何?解:(1)当时,; (2)当时,. 2、本题若修改为求函数的最值,讨论又该怎样进行? 解:(1)当时,,;(2)当时, ,;(3)当时,,;(4)当时, ,. 【解后反思】当二次函数开口向上时,(1)求给定区间的最小值,按对称轴与区间的三种位置关系讨论;(2)求最大值时,按对称轴与区间中点的位置关系分类讨论;(3)既求最大又求最小时,分四种情况讨论.在讨论的过程中要注意结合函数的图像.例 3 求函数在区间上的最小值.【分析】定轴动区间也按对称轴与区间的位置关系讨论.解:对称轴,(1)当即时,;(2)当即时,;(3)当即时,.例 4 讨论函数的最小值.解:,这个函数是一个分段函数,由于上下两段上的对称轴分别为直线,,当,,时原函数的图象分别如下(1),(2),(3)因此,(1)当时,; (2)当时,; (3)当时,【解后反思】本题突出体现了数形结合与分类讨论思想的有机结合.三、理解数学:1.已知二次函数满足条件及(1)求;(2)求在区间上的最大值和最小值.解:(1)设,由,可知, ,故由得,,因而, 所以;(2), ,所以当时,...