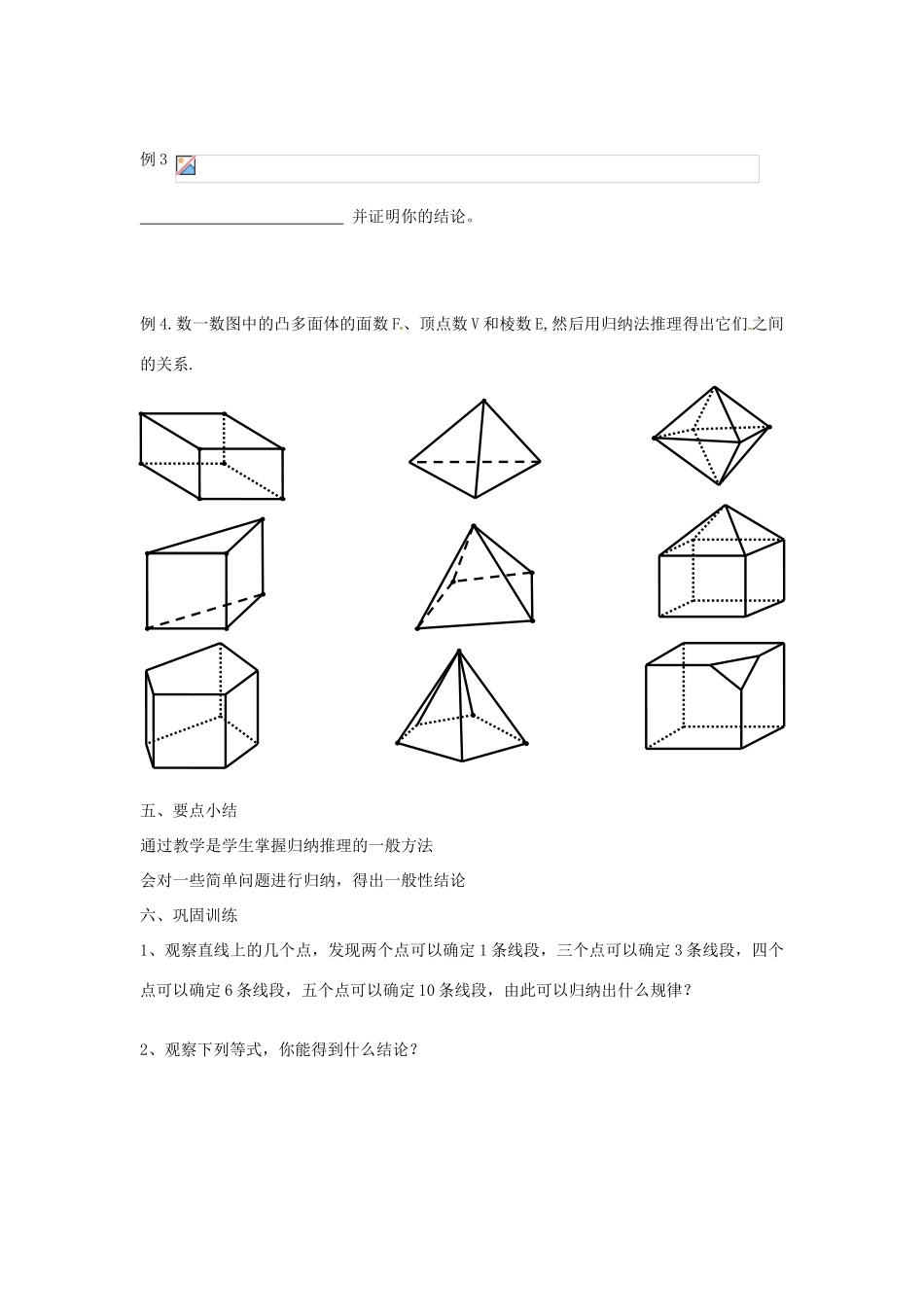
第 54 课时 归纳推理一、激趣导学(1)西汉时期的马王堆女尸,距今已将近 2200 年,是根据同位素的半衰期的推测的。(2)哥德巴赫,德国数学家。1742 年 6 月 7 日,他在写给著名数学家欧拉的一封信中,提出了两个大胆的猜想:(一)任何不小于 6 的偶数,都 是两个奇质数之和:(二)任何不小于 9 的奇数,都是 3 个奇质数之和。这就是数学史上著名的“哥德巴赫猜想”。 (三)蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的,蛇、鳄鱼、海归、蜥蜴都是爬行动物,所以,所有的爬行动物都是用肺呼吸的。 (四)教师从口袋里第一次拿出一块糖,第二次又拿出一块糖,第三次又拿出一块糖,第四次……。二、重点讲解这种由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理.归纳推理是由….到…..,由….到…..归纳推理的一般模式:S1 具有 P,S2 具有 P,Sn 具有 P(是 A 类事物的对象),所以,A 类事物具有 P。三、设疑讨论归纳推理三、典题拓展例 1 三角形的内角和是 1800,凸四边形的内角和是 3600,凸五边形的内角和是 5400,请猜想:凸 n 边形的内角和是 例 2 由此我们猜想: 例 3 并证明你的结论。例 4.数一数图中的凸多面体的面数 F、顶点数 V 和棱数 E,然后用归纳法推理得出它们 之间的关系.五、要点小结通过教学是学生掌握归纳推理的一般方法会对一些简单问题进行归纳,得出一般性结论六、巩固训练1、观察直线上的几个点,发现两个点可以确定 1 条线段,三个点可以确定 3 条线段,四个点可以确定 6 条线段,五个点可以确定 10 条线段,由此可以归纳出什么规律?2、观察下列等式,你能得到什么结论?4、观察下列数的特点 1,2,2,3,3,3,4,4,4,4,… 中,第 100 项是 ;5、 观察下列数:1,3,2,6,5,15,14,x,y,z,122,…中 x,y,z 的值依次是 ;6、依次有下列等式:,按此规律下去,第 8 个等式为 。7、已知数列{an}的第 1 项 a1=1 且(n=1,2,3 …),试归纳 出这个数列的通项公式。