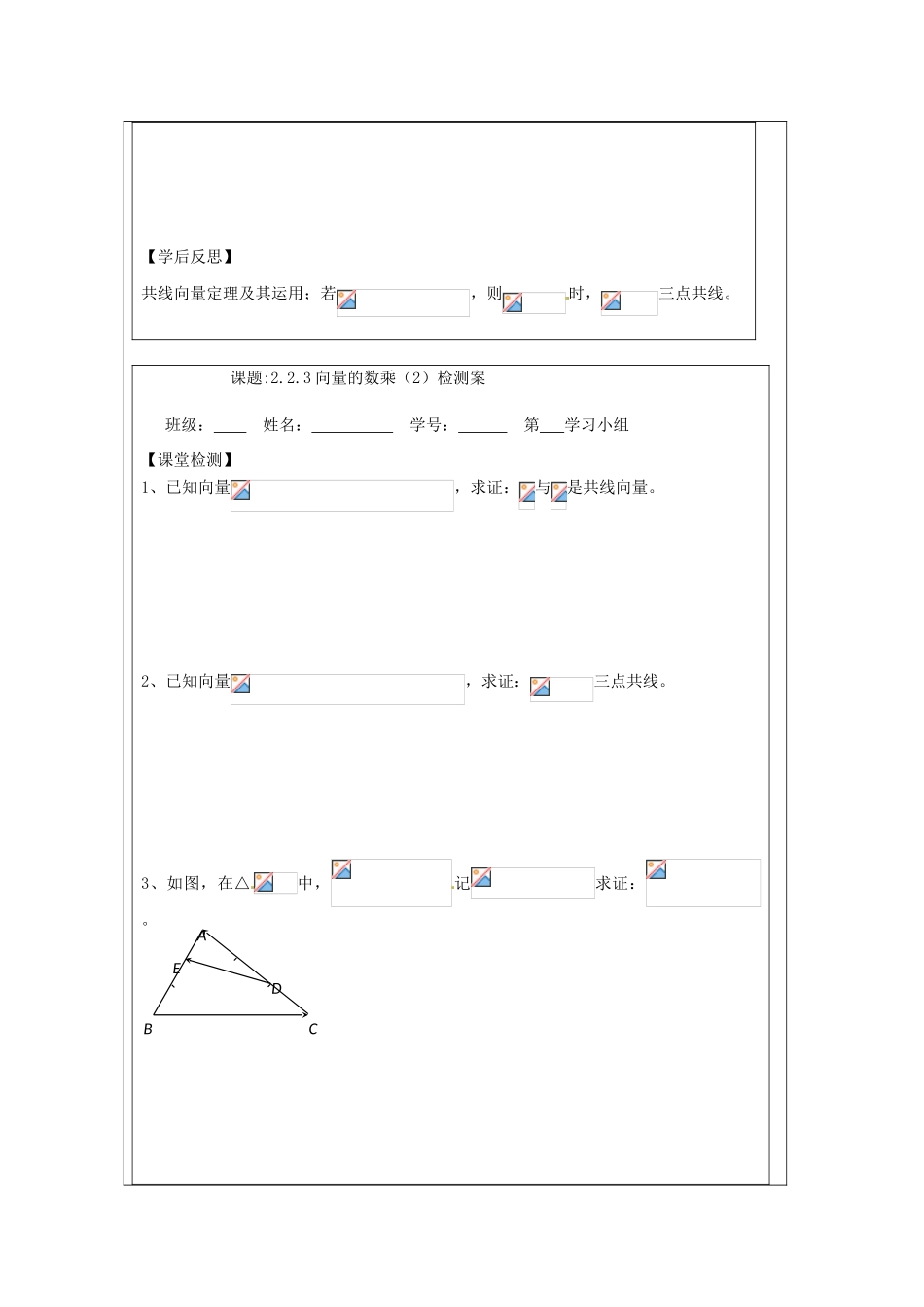
江苏省建陵高级中学 2013-2014 学年高中数学 2.2.3 向量的数乘(1)导学案(无答案)苏教版必修 4【学习目标】1、理解两个向量共线的含义,并掌握向量共线定理;2、能运用实数与向量的积解决有关问题。【课前预习】1、填空:(1) ;(2)当时,与方向 ;当时,与方向 ;当时,= ;当时,= 。(3) ; ; 。( 4 ) 若 向 量与方 向 相 反 , 且, 则与的 关 系 是 。(5)设是已知向量,若,则 。2、如图,,分别是的边、的中点,求证:与共线,并将用线性表示。3 、 共 线 向 量 定 理 : 如 果 存 在 一 个 实 数, 使 ,, 那 么 。反之,如果与是共线向量,那么 。注意:可写成,但不能写成或。4、提问:上述定理中,若无条件,会有什么结果?ABCDE5、向量共线定理如何用来解决点共线或线共点问题。【课堂研讨】例 1、设是非零向量,若,试问:向量与是否共线?例 2、如图,中,为直线上一点,,求证:。思考:上例证明的结论表明:起点为,终点为直线上一点的向量可以用表示。那么两个不共线的向量可以表示平面内任一向量吗?ABCO【学后反思】共线向量定理及其运用;若,则时,三点共线。 课题:2.2.3 向量的数乘(2)检测案班级: 姓名: 学号: 第 学习小组【课堂检测】1、已知向量,求证:与是共线向量。2、已知向量,求证:三点共线。3、如图,在△中,记求证:。ABCDE4、如图,设点是线段的三等分点,若,试用表示向量【课后巩固】1、点在线段上,且,设,则 ( ) A、 B、 C、 D、2、若是平行四边形的中心,且,则 ( ) A、 B、 C、 D、3、已知向量,则与 (填“共线”或“不共线”)。4、给出下列命题:①若,则;②若,则∥;③若,则;④则∥。其中,正确的序号是 。5、若是△的重心,则 。6、已知,则 三点共线。7、已知非零向量和不共线,若和共线,求实数的值。ABQPO8、设分别是的边上的点,且,,。若记,试用表示。 9、如图,平行四边形中,是的中点,交于,试用向量的方法证明:是的一个三等分点。课题:2.2.3 向量的数乘(2)班级: 姓名: 学号: 第 学习小组【学习目标】1、理解两个向量共线的含义,并掌握向量共线定理;2、能运用实数与向量的积解决有关问题。【课前预习】1、填空:(1) ;(2)当时,与方向 ;当时,与方向 ;当时,= ;当时,= 。(3) ; ; 。ABCDME(4)若向量与方向相反,且,则与的关系是 。(5)设是...