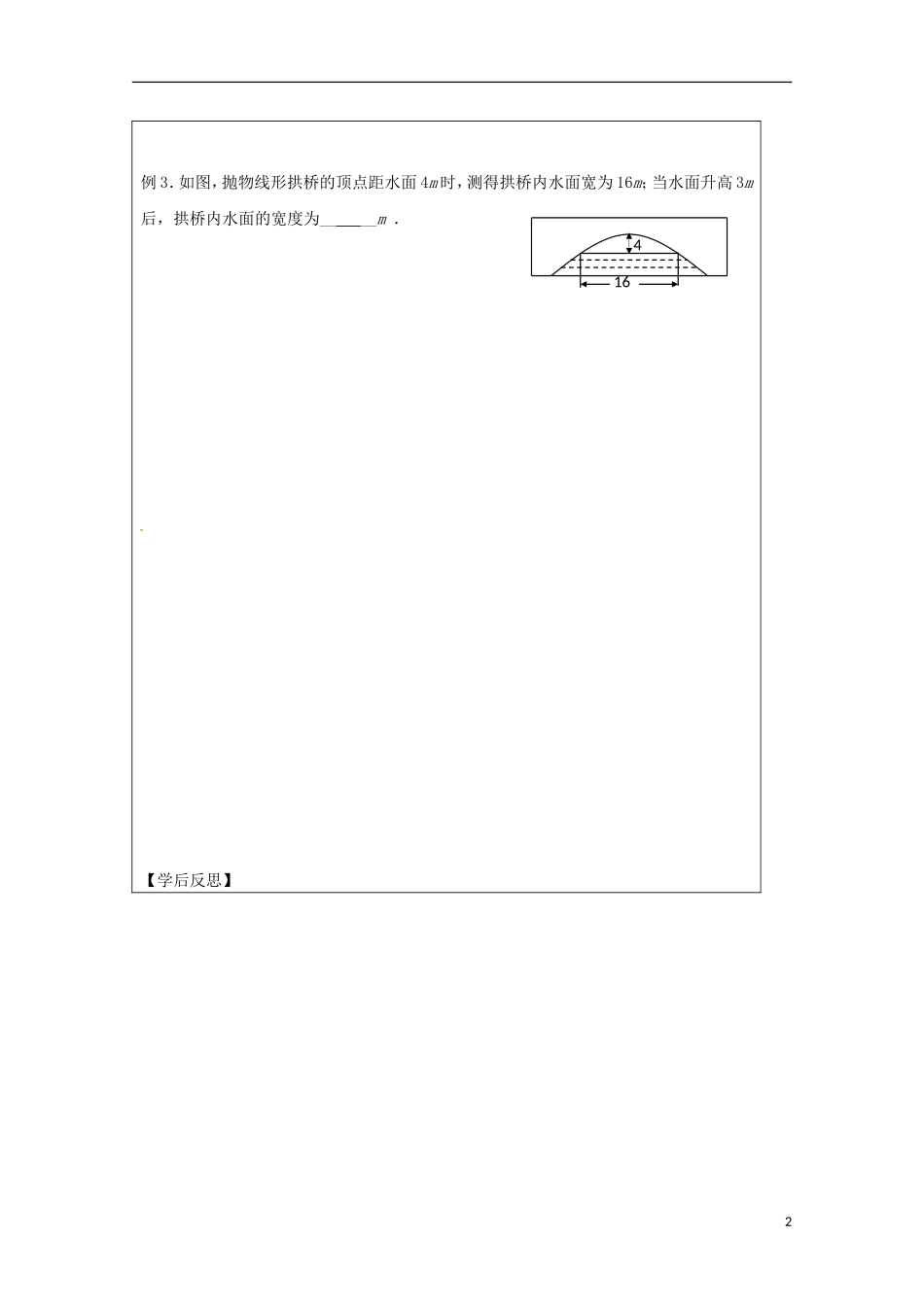
江苏省建陵高级中学 2013-2014 学年高中数学 2.4.2 抛物线的几何导学案(无答案)苏教版选修 1-1【学习目标】1.掌握抛物线的简单几何性质;2.能根据抛物线方程解决简单的应用问题【课前预习】1.类比椭圆、双曲线来填写下表图形标准方程焦点坐标准线方程【合作探究】 [例 1]若抛物线上一点到准线及对称轴的距离分别为 10 和 6,求P 的横坐标及抛物线方程. [例 2]给定抛物线,设,是抛物线的一点,且,试求的最小值.1例 3.如图,抛物线形拱桥的顶点距水面 4m 时,测得拱桥内水面宽为 16m;当水面升高 3m后,拱桥内水面的宽度为__ __m .【学后反思】2164课题:2.4.1 抛物线的几何性质检测案 班级: 姓名: 学号: 第 学习小组【课堂检测】1.若抛物线上一点 A 的纵坐标是 4,则 A 点到焦点 F 的距离为___2.若抛物线)0(22ppyx上纵坐标为4的点到焦点的距离为5 ,则焦点到准线的距离是 . 3. 抛物线上一点到焦点的距离为 3,则点到轴的距离为 【课后巩固】1、抛物线上到其准线和顶点距离相等的点的坐标为 ________. 2.已知点 P 在抛物线上,那么点 P 到点的距离与点 P 到抛物线焦点距离之和取得最小值时,点 P的坐标为 .3、已知是抛物线上的动点, 是抛物线的焦点,则线段的中点轨迹方程是 34、抛物线xy22 关于直线01 yx对称的抛物线方程是 。5.已知圆 x2+y2-6x-7=0 与抛物线 y2=-2px (p>0)的准线相切,则 p= . 6.已知抛物线的顶点在原点,对称轴是 x轴,抛物线上的点 M(-3,m)到焦点的距离等于 5,求抛物线的方程和 m 的值4