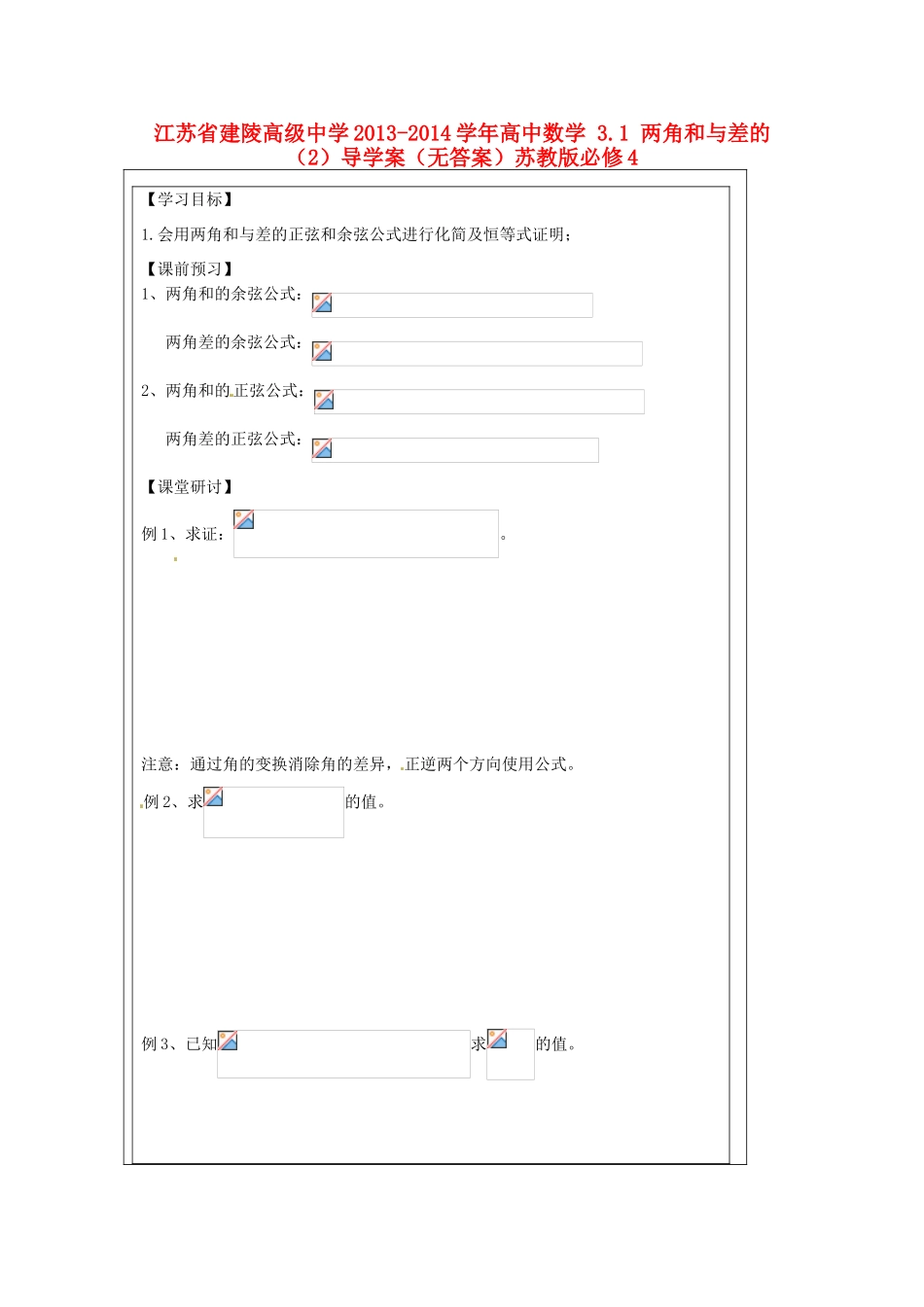
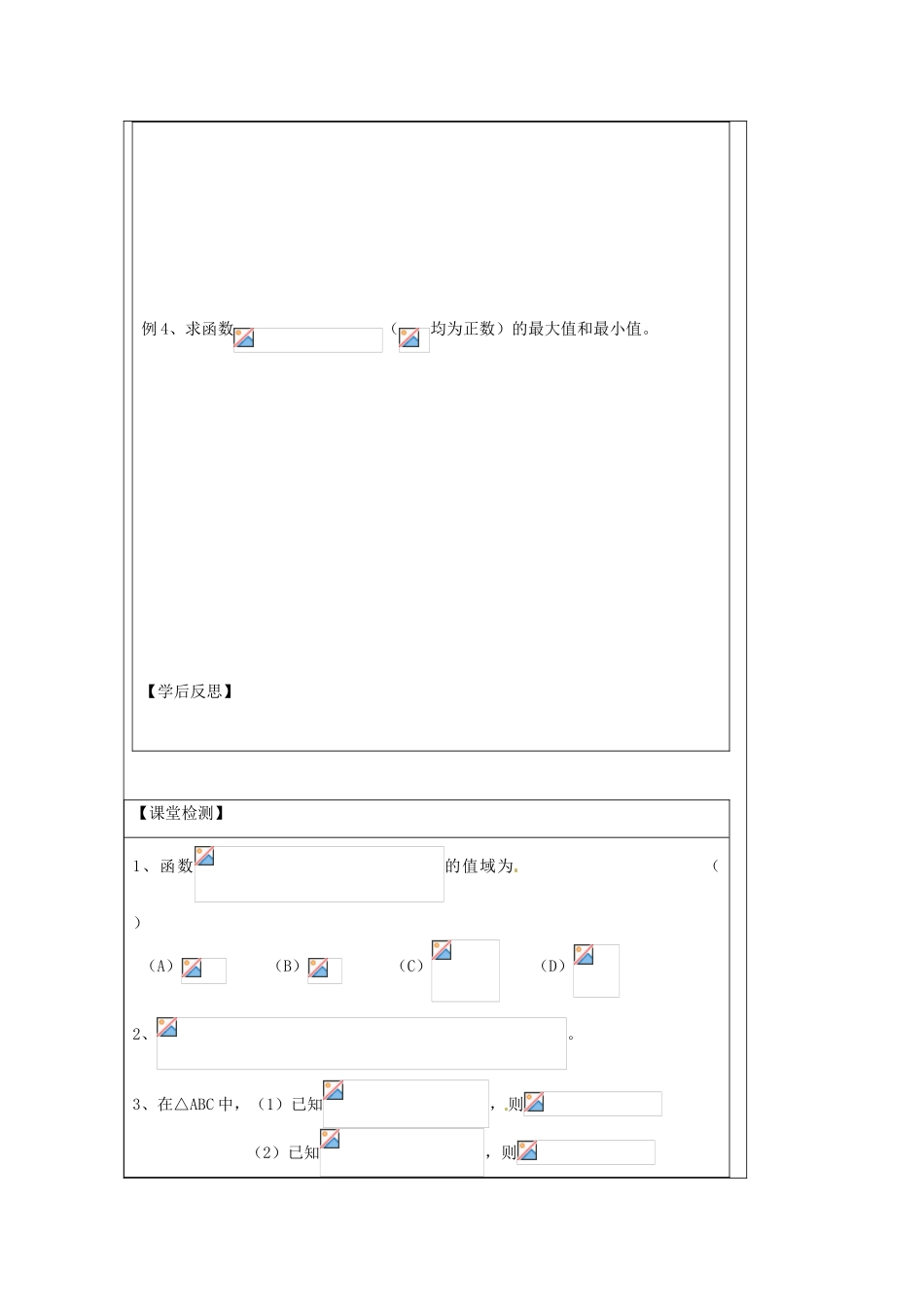
江苏省建陵高级中学 2013-2014 学年高中数学 3.1 两角和与差的(2)导学案(无答案)苏教版必修 4【学习目标】1.会用两角和与差的正弦和余弦公式进行化简及恒等式证明;【课前预习】1、两角和的余弦公式: 两角差的余弦公式:2、两角和的正弦公式:两角差的正弦公式:【课堂研讨】例 1、求证:。 注意:通过角的变换消除角的差异,正逆两个方向使用公式。例 2、求的值。例 3、已知求的值。例 4、求函数(均为正数)的最大值和最小值。【学后反思】【课堂检测】1、函数的值域为 ( ) (A) (B) (C) (D) 2、。3、在△ABC 中,(1)已知,则 (2)已知,则 【课后作业】1 求证: (1); (2)。2、已知都为锐角,。(1)试用与表示角;(2)求与的值。3.已知求的值。课题: 3.1 两角和与差的正弦、余弦班级: 姓名: 学号: 第 学习小组【学习目标】1.会用两角和与差的正弦和余弦公式进行化简及恒等式证明;【课前预习】1、两角和的余弦公式: 两角差的余弦公式:2、两角和的正弦公式:两角差的正弦公式:【课堂研讨】例 1、求证:。 注意:通过角的变换消除角的差异,正逆两个方向使用公式。例 2、求的值。例 3、已知求的值。例 4、求函数(均为正数)的最大值和最小值。【学后反思】【课堂检测】1、函数的值域为 ( ) (A) (B) (C) (D) 2、。3、在△ABC 中,(1)已知,则 (2)已知,则【课后作业】1 求证: (1); (2)。2、已知都为锐角,。(1)试用与表示角;(2)求与的值。3.已知求的值。