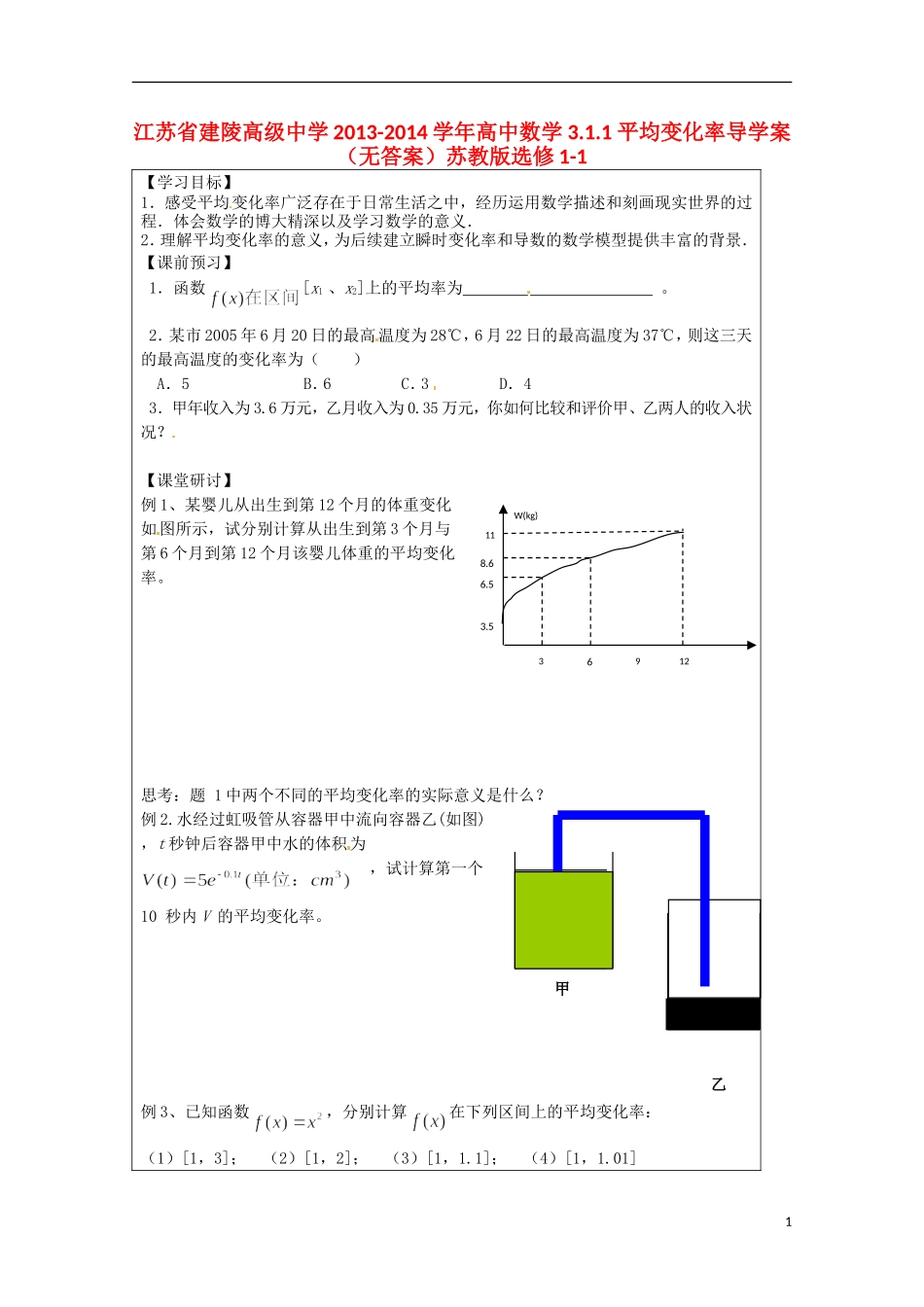
江苏省建陵高级中学 2013-2014 学年高中数学 3.1.1 平均变化率导学案(无答案)苏教版选修 1-1【学习目标】1.感受平均变化率广泛存在于日常生活之中,经历运用数学描述和刻画现实世界的过程.体会数学的博大精深以及学习数学的意义.2.理解平均变化率的意义,为后续建立瞬时变化率和导数的数学模型提供丰富的背景.【课前预习】1.函数[x1 、x2]上的平均率为 。2.某市 2005 年 6 月 20 日的最高温度为 28℃,6 月 22 日的最高温度为 37℃,则这三天的最高温度的变化率为( )A.5B.6C.3D.43.甲年收入为 3.6 万元,乙月收入为 0.35 万元,你如何比较和评价甲、乙两人的收入状况?【课堂研讨】例 1、某婴儿从出生到第 12 个月的体重变化如图所示,试分别计算从出生到第 3 个月与第 6 个月到第 12 个月该婴儿体重的平均变化率。思考:题 1 中两个不同的平均变化率的实际意义是什么?例 2.水经过虹吸管从容器甲中流向容器乙(如图) ,t 秒钟后容器甲中水的体积为 ,试计算第一个10 秒内 V 的平均变化率。例 3、已知函数,分别计算在下列区间上的平均变化率: (1)[1,3]; (2)[1,2]; (3)[1,1.1]; (4)[1,1.01]1甲W(kg)639123.56.58.611乙例 4、已知函数 f (x) = 2x + 1,g(x) = -2x,分别计算在下列区间上函数 f(x)及 g(x)的平均变化率.(1)[-3,-1]; (2)[0,5]【学后反思】2课题:3.1.1 平均变化率班级: 姓名: 学号: 第 学习小组【课堂检测】1.“十·一”黄金周的七天时间里,本市某大型商场的日营业额从 1500 万元增加到4200 万元,则该商场黄金周期间日营业额的平均变化率为____________万元/日2.函数在区间[0,1]上的平均变化率是__________ 3.函数在区间[1,3]上的 平均变化率是 .4.函数在区间[1,m]上的平均变化率为 3,则 m 的值为 .【课后作业】1.已知正方形原来的边长为 4m,现在边长以 2m/s 的速度增加,若设正方形的面积为3S(单位:m2),时间为 t(单位:s),则由时间 t(s)到 t+l(s)时正方形的面积增加了 。2.现有一质量分布不均匀的细棒长 20cm,从细棒 A 端起,至棒上任意一点 M 的质量与AM 的长度的平方成正比,又测得自 A 端 8cm 长的一段的质量是 64g,(1)若 AM0=2 cm,那么该段细棒的质量为多少?(2)求 AM 的长度由 x0增加到 x0+△x 质量的平均变化率。3.某工厂 8 年来生产某种新产品的总数...