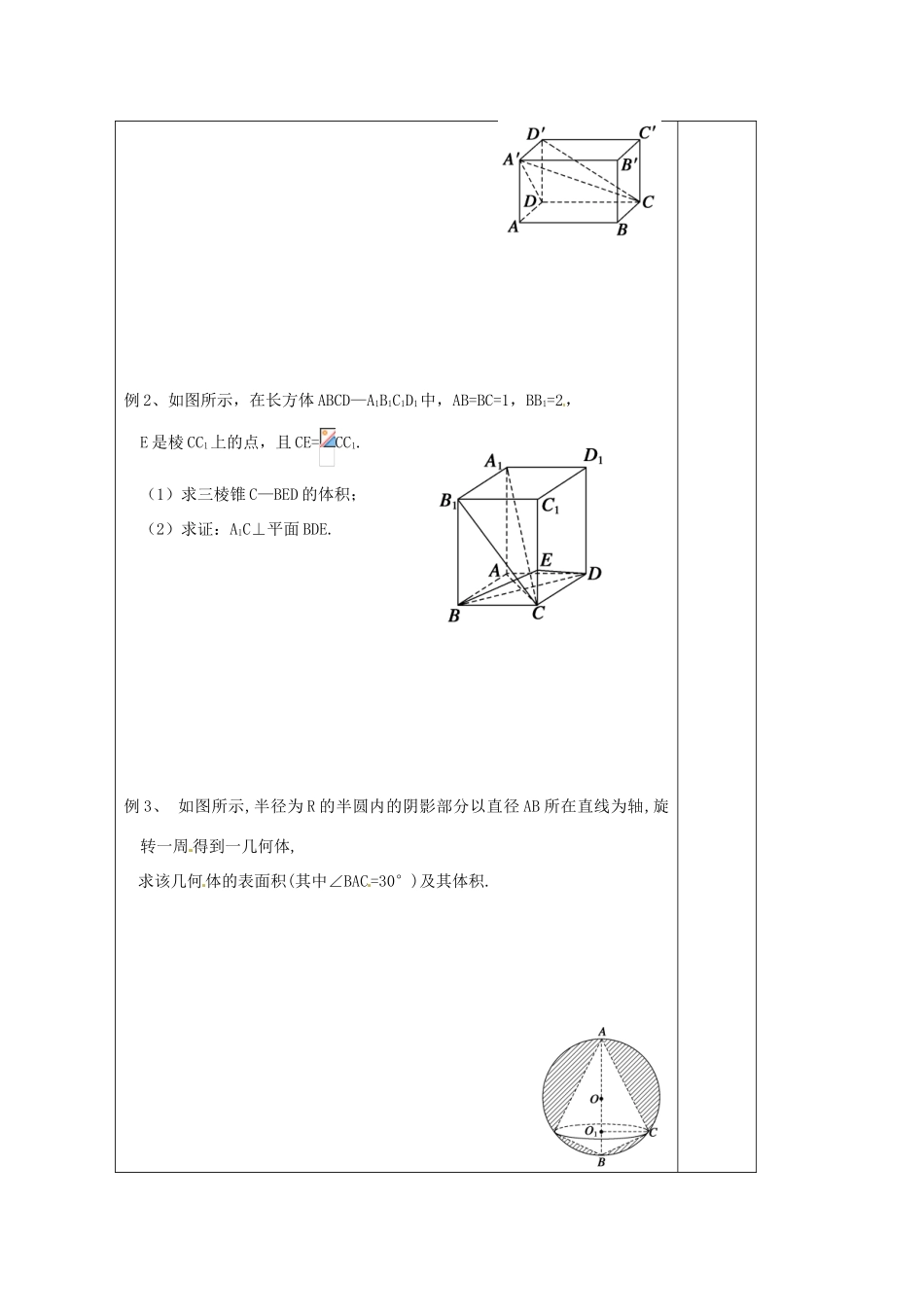
江苏省建陵高级中学 2014 届高考数学一轮复习 空间几何体表面积体积导学案一:学习目标柱、锥、台、球的表面积与体积二:课前预习1.三棱锥 S—ABC 中,面 SAB,SBC,SAC 都是以 S 为直角顶点的等腰直角三角形,且 AB=BC=CA=2,则三棱锥 S—ABC 的表面积是 .2.如图所示,在棱长为 4 的正方体 ABCD-A1B1C1D1中,P 是 A1B1上一点,且 PB1=A1B1,则多面体 P-BCC1B1的体积为 .3.已知正方体外接球的体积为,那么正方 体的棱长等于 .4.如图所示,在直三棱柱 ABC-A1B1C1 中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1=.P 是 BC1上一动点,则 CP+PA1的最小值是 .5. 如图所示,E、F 分别是边长为 1 的正方形 ABCD 边 BC、CD 的中点,沿线AF,AE,EF 折起来,则所围成的三棱锥的体积为 .三:课堂研讨例 1 如图所示,长方体 ABCD—A′B′C′D′中,用截面截下一个棱锥C—A′DD′,求棱锥 C—A′DD′的体积与剩余部分的体积之比.备 注例 2、如图所示,在长方体 ABCD—A1B1C1D1中,AB=BC=1,BB1=2,E 是棱 CC1上的点,且 CE=CC1.(1)求三棱锥 C—BED 的体积;(2)求证:A1C⊥平面 BDE.例 3、 如图所示,半径为 R 的半圆内的阴影部分以直径 AB 所在直线为轴,旋转一周 得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.课堂检测——空间几何体的表面积体积 姓名: 1.若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的表面积是 .2.如图所示,扇形的中心角为 90°,其所在圆的半径为 R,弦 AB 将扇形分成两个部分,这两部分各以 AO 为轴旋转一周,所得旋转体的体积 V1和 V2之比为 .3.长方体的过一个顶点的三条棱长的比是 1∶2∶3,对角线长为 2,则这个长方体的体积是 .4.如图所示,三棱锥 A—BCD 一条侧棱 AD=8 cm,底面一边 BC=18 cm,其余四条棱的棱长都是 17 cm,求三棱锥 A—BCD 的体积.课外作业——空间几何体的表面积体 姓名: 1.已知各顶点都在一个球面上的正四棱柱高为 4,体积为 16,则这个球的表面积是 .2.一个正三棱锥的四个顶点都在半径为 1 的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 .3.已知一个凸多面体共有 9 个面,所有棱长均为 1,其平 面 展 开 图 如 图 所 示 , 则 该 凸 多 面 体 的 体 积 V= .4.在长方体 ABCD-A1B1C1D1中,AB=BC=2,过 A1、C1、B 三点的平面截去长方体的一个角后,得到如图所示的几何体 ABCD-A1C1D1,且这个几何体的体积为.(1)证明:直线 A1B∥平面 CDD1C1;(2)求棱 A1A 的长;(3)求经过 A1,C1,B,D 四点的球的表面积.