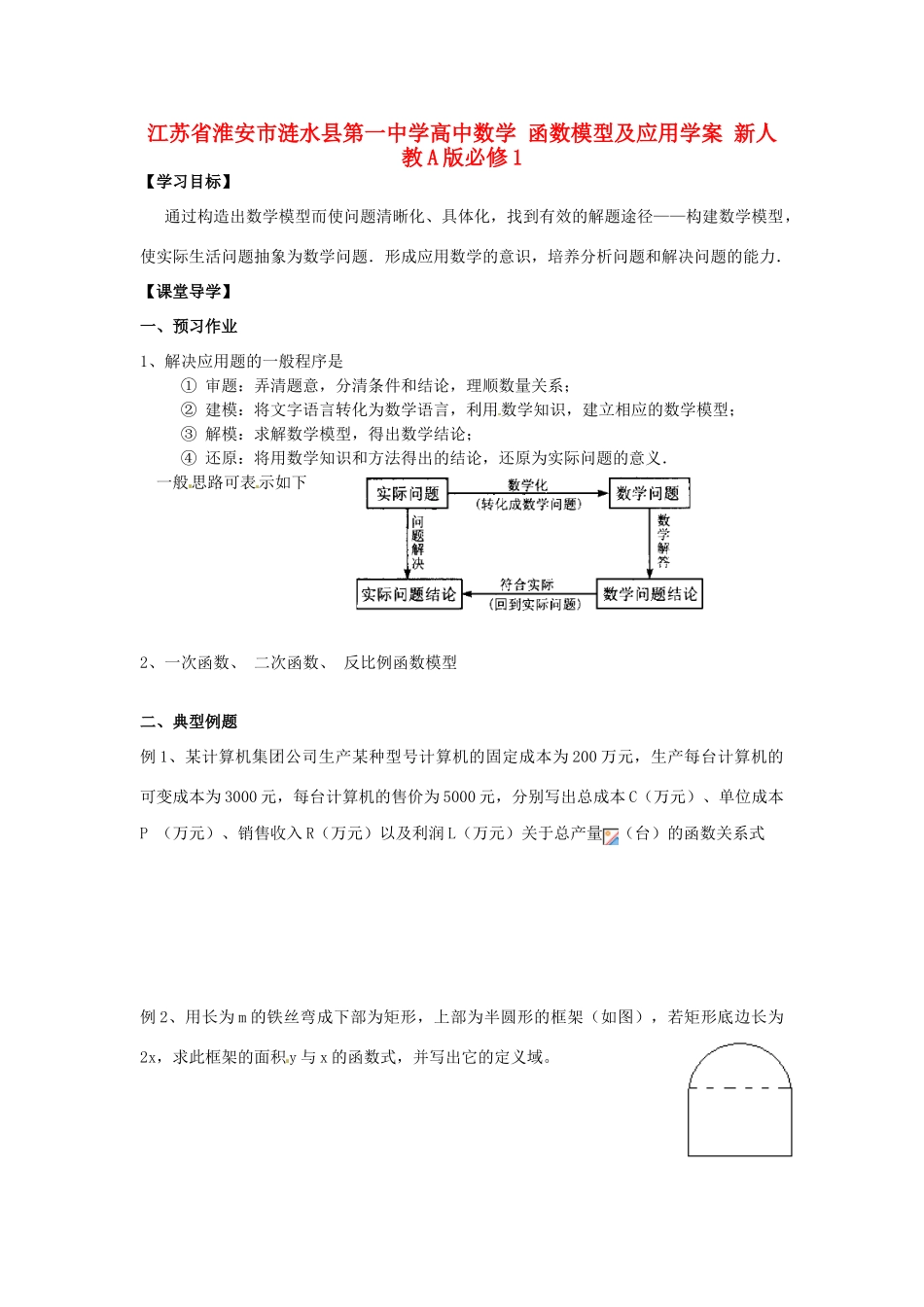
江苏省淮安市涟水县第一中学高中数学 函数模型及应用学案 新人教 A 版必修 1【学习目标】通过构造出数学模型而使问题清晰化、具体化,找到有效的解题途径——构建数学模型,使实际生活问题抽象为数学问题.形成应用数学的意识,培养分析问题和解决问题的能力.【课堂导学】一、预习作业1、解决应用题的一般程序是 ① 审题:弄清题意,分清条件和结论,理顺数量关系; ② 建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型; ③ 解模:求解数学模型,得出数学结论;④ 还原:将用数学知识和方法得出的结论,还原为实际问题的意义.一般思路可表示如下2、一次函数、 二次函数、 反比例函数模型二、典型例题例 1、某计算机集团公司生产某种型号计算机的固定成本为 200 万元,生产每台计算机的可变成本为 3000 元,每台计算机的售价为 5000 元,分别写出总成本 C(万元)、单位成本P (万元)、销售收入 R(万元)以及利润 L(万元)关于总产量(台)的函数关系式例 2、用长为 m 的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架的面积y 与 x 的函数式,并写出它的定义域。例 3、某商店如将进价 8 元的商品按每件 10 元出售,每天可销售 200 件。现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价 0.5 元,其销售量就减少 10 件,问应将售价定为多少时,才能使所赚利润最大,并求出最大利润。1、 某地高山上温度从山脚起每升高 100m 降低 0. 7oC,已知山顶的温度是 14.1oC,山脚的温度是 26oC。问:此山高为________一、填空题1、某种细胞 分裂时,由 1 个分裂成 2 个,2 个分裂成 4 个,……, 1 个细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系式是。其中 x 的取值范围是_________________2、某单位为鼓励职工节约用水,做出了如下规定:每月用水不超过 10m3,按每立方米 1 元收取水费;每月用水超过 10m3,超过部分加倍收费。某职工某月缴水费 16 元,则该职工这月实际用水为_________________。3、一个长方体容器的底面为边长是 acm 的正方形,高度为 hcm,现以每秒 dcm3的速度注入某种溶液,则容器内溶液的高度 y(cm)与注入时间 t(s)的函数关 系式是_________________。4、有一块边长为 a 的正方形铁皮,将其四个角各截支一个边长为 x 的小正方形,然后拆成一个无盖的盒子,则盒子的...