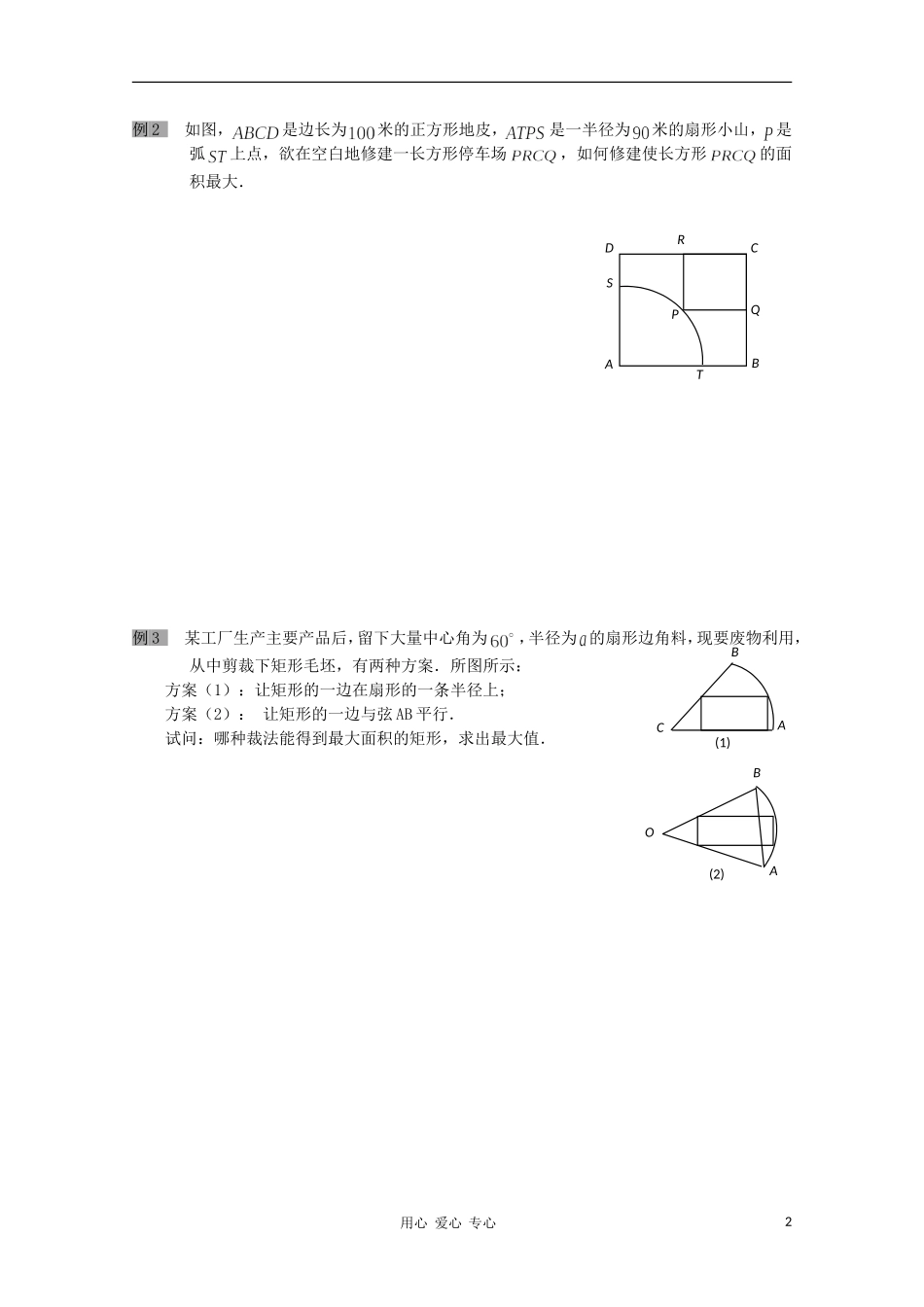
总 课 题解三角形总课时第 6 课时分 课 题正余弦定理的应用(二)分课时第 2 课时教学目标利用正余弦定理来解决有关三角形中的问题;会利用数学建模的思想,结合解三角形知识解决生产实践中的几何问题;学会对信息进行收集,加以整理,提高分析问题,解决问题的能力.重点难点正余弦定理在实际问题中的应用;建立三角函数模型.引入新课引入新课1.四边形是半径为的圆内接矩形,求矩形面积的最大值.2.已知一个直角三角形的周长为 ,求其斜边长的最小值.例题剖析例题剖析例 1 如图,半圆的直径为 , 为直径延长线上的一点,, 为半圆上任意一点,以为一边作等边,问点在什么位置时,四边形的面积最大?用心 爱心 专心1例 2 如图,是边长为米的正方形地皮,是一半径为米的扇形小山, 是弧上点,欲在空白地修建一长方形停车场,如何修建使长方形的面积最大.例 3 某工厂生产主要产品后,留下大量中心角为,半径为 的扇形边角料,现要废物利用,从中剪裁下矩形毛坯,有两种方案.所图所示:方案(1):让矩形的一边在扇形的一条半径上;方案(2): 让矩形的一边与弦 AB 平行.试问:哪种裁法能得到最大面积的矩形,求出最大值.用心 爱心 专心2ABPQRDCTSOBA(2)ABC(1)课堂小结课堂小结正余弦定理在实际问题中的应用;建立三角函数模型.用心 爱心 专心3课后训练课后训练班级:高一( )班 姓名:____________一 基础题1.中,角的对边分别为,那么等于( ) A.B.C.D. 2.在中,,则 ( ) A.B.C.D.3.在中,若的面积为 ,且,则___________.二 提高题4.把一根长为的木条锯成两段,分别作钝角三角形的两边和,且,如何锯断木条,才能使第三条边最短.5.如图,已知为定角,分别在的两边上,为定长,当处于什么位置时,的面积最大?用心 爱心 专心4AQP6.在中,已知,,,求 .三 能力题7.内以为圆心, 为半径的圆,且,(1)求·,·,·;(2)求.8.在中,已知,,求证:为正三角形时其周长取得最大值.用心 爱心 专心5