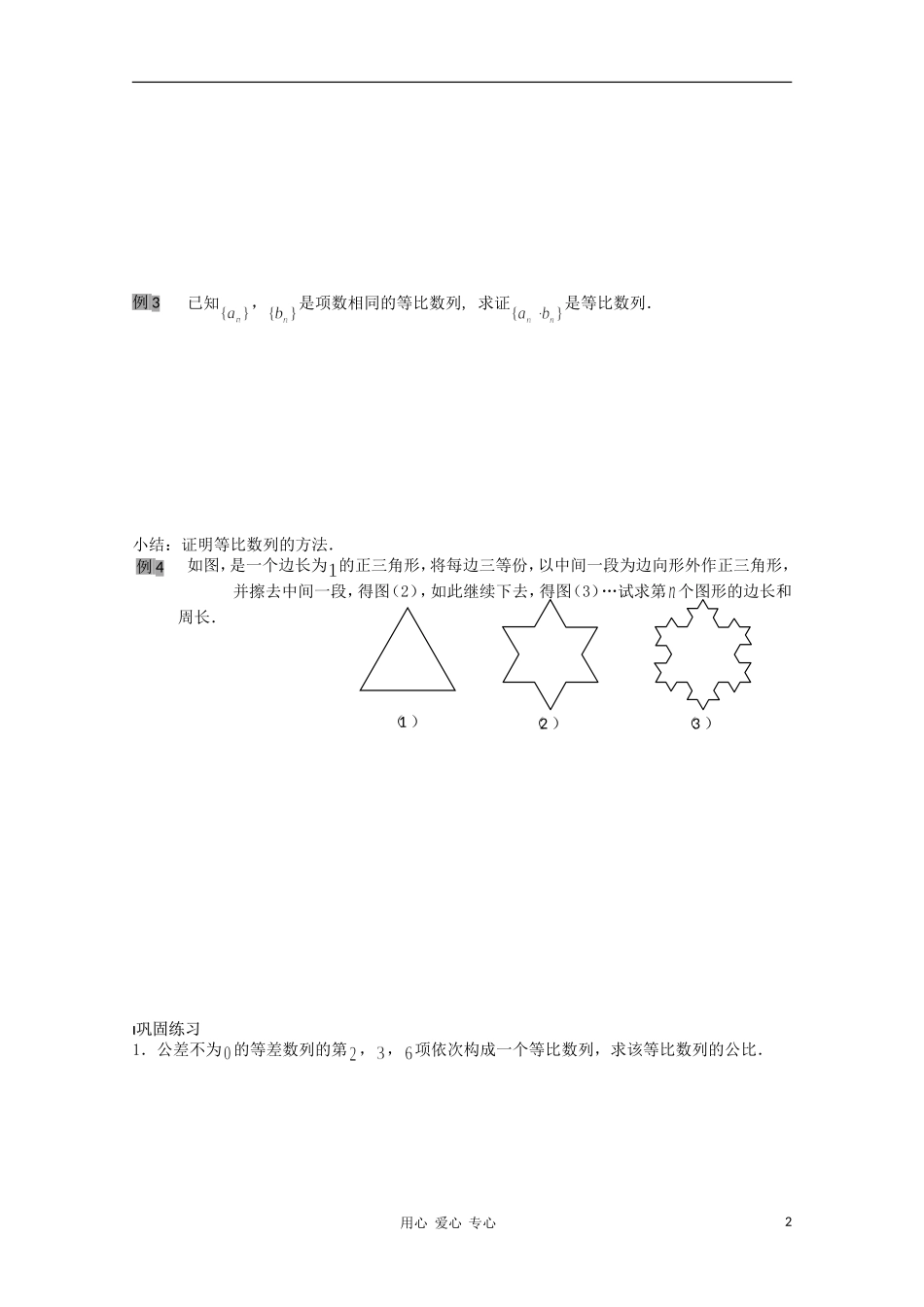
总 课 题等比数列总课时第 14 课时分 课 题等比数列(二)分课时第 2 课时教学目标能运用等比数列的概念及其通项公式解决问题;理解等比中项的意义.重点难点等比数列的概念及通项公式的应用.引入新课引入新课1.判断:(1)已知,则成等比数列.( )(2)已知,则成等比数列.( )(3)已知成等比数列,则成等差数列.( )(4)已知成等差数列,则成等比数列.( )例题剖析例题剖析已知等比数列的通项公式是,求首项和公比 ,并画出该数列的图像.已 知是 公 比 为的 等 比 数 列 , 新 数 列也是等比数列吗?练习:已知无穷等比数列的首项为,公比为 ,(1)依次取出数列中的所有奇数项,组成一个新数列,这个数列还是等比数列吗? 如果是,它的首项和公比是多少? (2)数列(其中常数)是等比数列吗? 如果是,它的首项和公比是多少?用心 爱心 专心1已知,是项数相同的等比数列, 求证是等比数列.小结:证明等比数列的方法.如图,是一个边长为 的正三角形,将每边三等份,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)…试求第 个图形的边长和周长.巩固练习巩固练习1.公差不为 的等差数列的第 , , 项依次构成一个等比数列,求该等比数列的公比.用心 爱心 专心2例 3 例 4 (1 )(2 )(3 )2.在等比数列中,(1)是否成立?是否成立?是否成立?总结一般结论: 3.若成等比数列,则称为 和 的等比中项.(1)和的等比中项为 ;(2)已知两个数和的等比中项是,则 .课堂小结课堂小结等比数列的概念及性质、通项公式的应用,等比中项概念.用心 爱心 专心3课后训练课后训练班级:高一( )班 姓名:____________一 基础题1.首项为 ,末项为,公比为 的等比数列的项数有 项.2.若 与 的等差中项是,则__________; 与 的等比中项是____________.3.在等比数列中,,则的值是___________.4.在各项均为正数的等比数列中,若,求的值.5.三个正数成公比大于 的等比数列,,,求.二 提高题6.三个数成等比数列,它们的积等于,它们的平方和等于,求这三个数.7.在等比数列中,,求.8.在等比数列中,,求.用心 爱心 专心4三 能力题9.如图,在边长为 的等边中,连结各边中点得,再连结各边中点得…如此继续下去,证明:是等比数列.10.某地现有耕地公顷,规划十年后粮食单产比现在增加,人均...