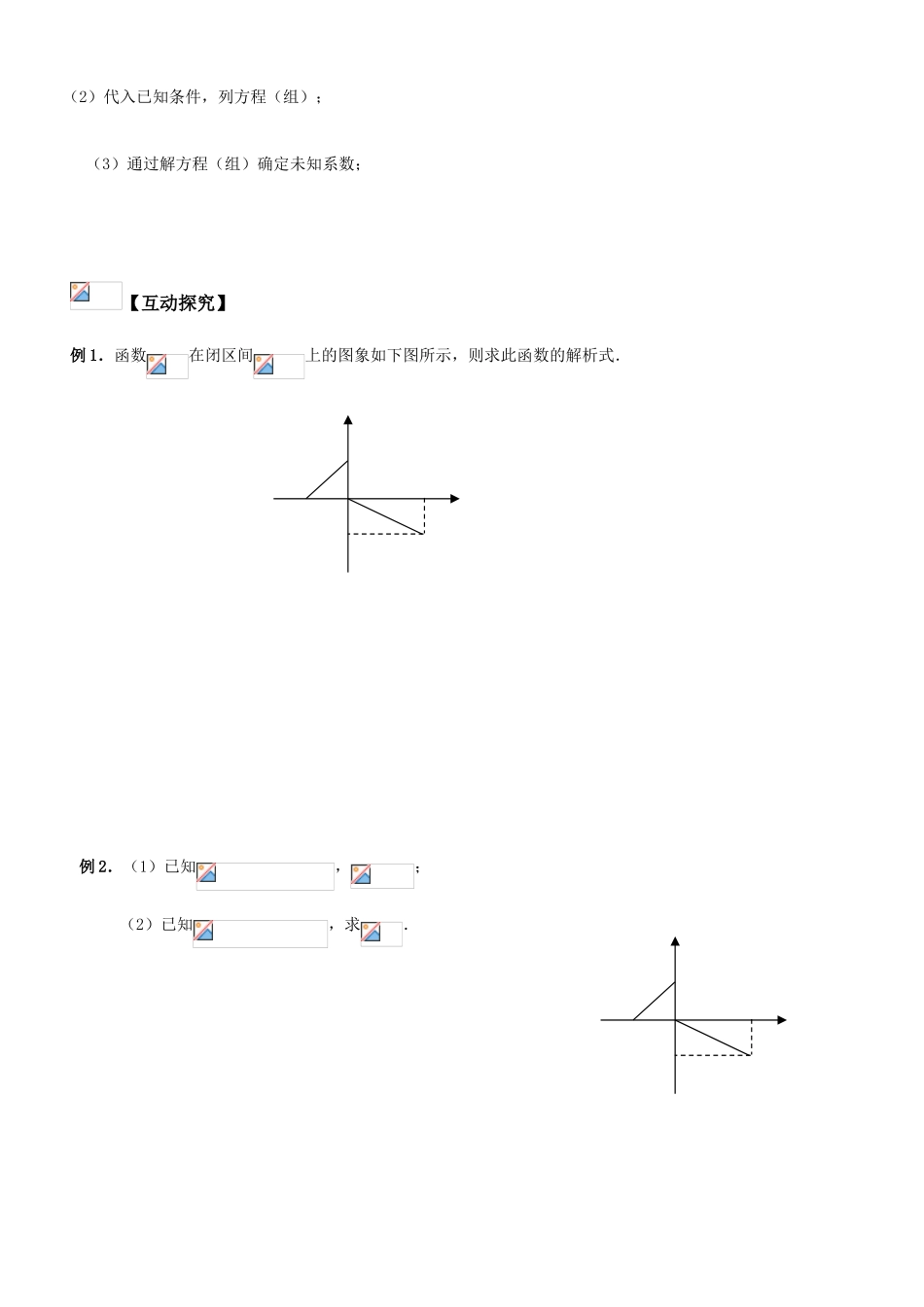
赣马高级中学 2010 级高一数学函数的表示方法(1)导学案【学习导航】 知识网络 学习目标 1.进一步理解和掌握表示两个变量之间的函数关系的方法——列表法、解析法、图象法; 2.能根据条件求出两个变量之间的函数解析式; 3.培养抽象概括能力和解决问题的能力.新课导学1.列表法的定义: 2.解析法的定义: 3.图像法的定义: 4.简述三种表示法的优缺点: 5.分段函数的定义: 6.二次函数的形式:(1)一般式: ;(2)交点式: ,其中,分别是的图象与轴的两个交点的横坐标;(3)顶点式:, 其中是抛物线顶点的坐标;7.已知函数类型,求函数解析式,常用待定系数法。例如,求二次函数解析式的基本步骤是:(1)设出函数的一般式(或顶点式、交点式);函数的表示方法列表法解析法图象法(2)代入已知条件,列方程(组);(3)通过解方程(组)确定未知系数;【互动探究】例 1.函数在闭区间上的图象如下图所示,则求此函数的解析式.例 2.(1)已知,; (2)已知,求.例 3.某人开汽车以的速度从地到远处的地,在地停留后,再以 的速度返回地,把汽车离开地的路程表示为时间(从地出发是开始)的函数,再把车速表示为时间的函数.例 4.已知一个函数的解析式为,它的值域为,这样的函数有多少个?试写出其中两个函数。【迁移应用】1、已知 a,b 为常数,若 f(x)=x2+4x+3,f(ax+b)=x2+10x+24,则 5a-b=_________.2.已知一个函数的解析式为,它的 值域为,这样的函数有多少个?试写出其中两个函数.3.若,则的解析式为 。4.已知,,则 , 。函数的表示方法(1)1.二次函数的形式:(1)一般式: ;(2)交点式: ,其中,分别是的图象与轴的两个交点的横坐标;(3)顶点式:, 其中是抛物线顶点的坐标;2.已知函数类型,求函数解析式,常用待定系数法。例如,求二次函数解析式的基本步骤是:(1)设出函数的一般式(或顶点式、交点式);(2)代入已知条件,列方程(组);(3)通过解方程(组)确定未知系数;3.分别求满足下列条件的二次函数 的解析式:(1)图象与轴的两交点为,,且;(2)图象的顶点是,且经过原点。答案:(1);(2)。例 1:函数在闭区间上的图象如下图所示,则求此函数的解析式.【解】由图象可知,当时,;当时,,所以例 2:(1)已知,; (2)已知,求.【解】(1); (2)。点评: 已知的解析式,求时,将中的用代替,这时中的相当于中一个取值;已知的解析式,...