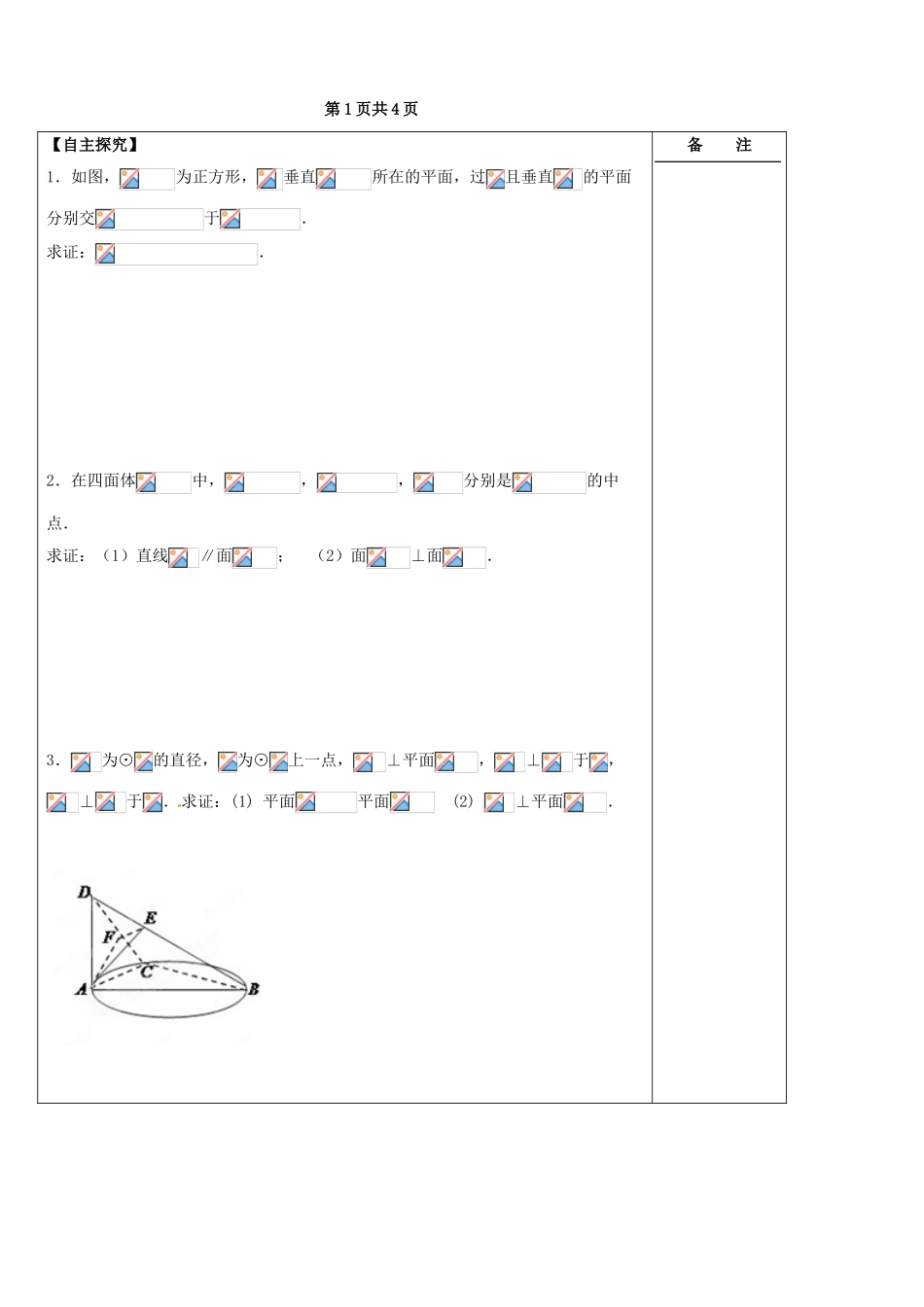
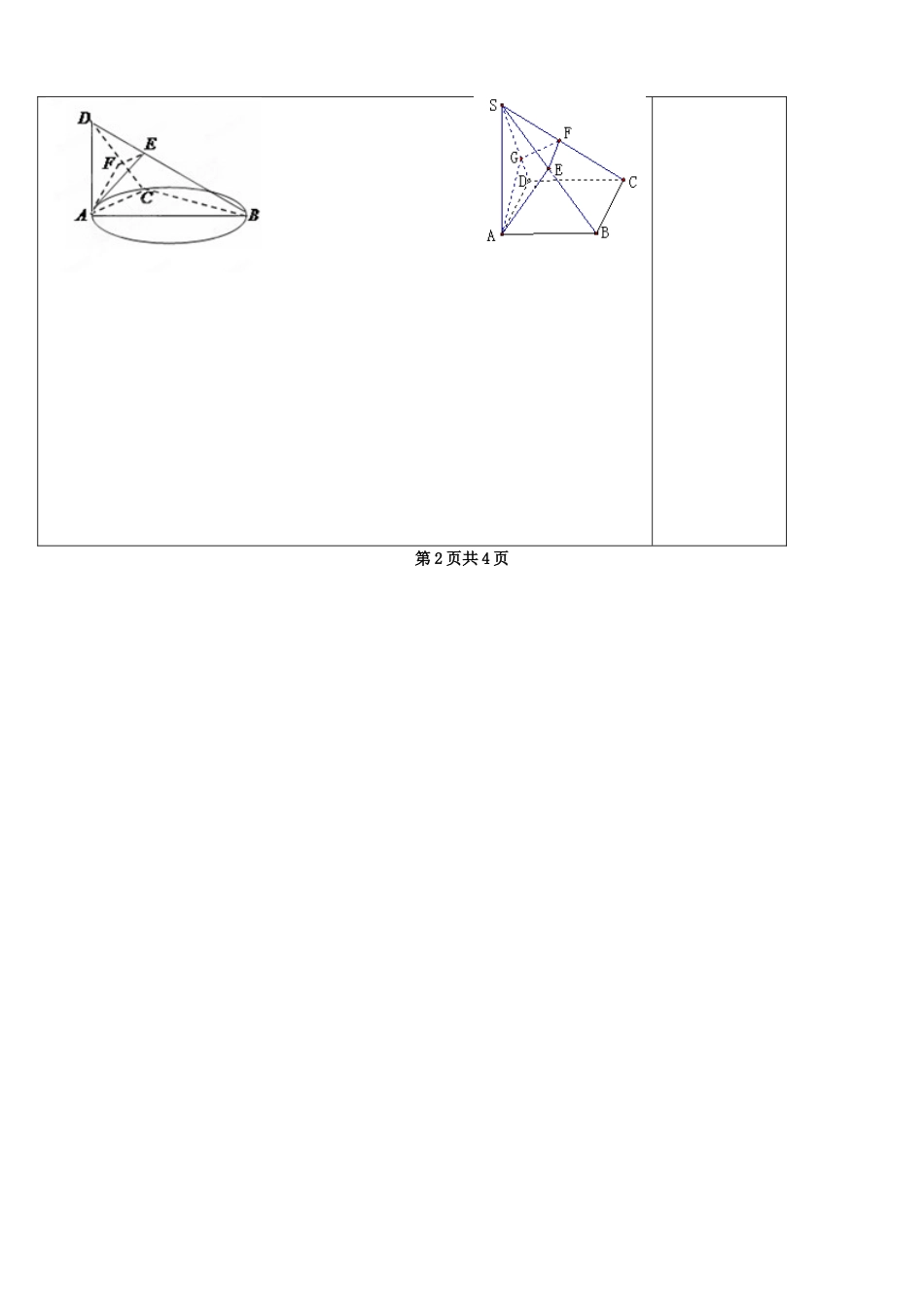
江苏省盐城市时杨中学 2014 届高考数学一轮复习 直线与平面的位置关系导学 案 2 【学习目标】掌握直线与平面平行、直线与平面垂直的定义、判定定理与性质定理,并能运用它们进行论证和解决有关问题.【问题情境】一、知识回顾:二、预习练习:1.若是互不相同的空间直线, 是不重合的 面,则下列命题中为真命题的是_____ ___.(1)若则 (2)若则 (3) 若则; (4) 若,则.2.“直线与平面内无数条直线垂直”是“直线与平面垂直”的___________ 条件.3.正方体中,分别是棱和上的点,若是直角,则=____________.4.设为两条直线,是两个平面,给出下列命题,真命题的有_______.(1)若; (2) 若;(3) 若; (4) 若.【我的疑问】备 注 第 1 页共 4 页 【自主探究】1.如图,为正方形,垂直所在的平面,过且垂直的平面分别交于.求证:.2.在四面体中,,,分别是的中点. 求证:(1)直线∥面; (2)面⊥面.3.为⊙的直径,为⊙上一点,⊥平面,⊥于, ⊥于.求证:(1) 平面平面 (2) ⊥平面.备 注第 2 页共 4 页【课堂检测】1.如果直线平面,下述判断正确的是_________.① 若直线,则∥; ②若,则∥ ;③ 若∥,则; ④若∥ ,则. 2.点不在三角形所在的平面内,过作平面,使三角形的三个顶点到的距离相等,这样的平面共有_____________个. 3.如图,在四棱锥中,底面是正方形,平面,且,点为的中点,点为的中点.求证:.【回标反馈】备 注 第 3 页共 4 页 【巩固练习】1.在正方体中,与正方体的一条对角线垂直的各面的对角线的条数是 .2.如图,在矩形中,=,,沿对角线将折起,使移动到,且在面内的射影恰好落在上.求证:(1) ; (2) 面.3.如图,已知垂直于矩形所在平面,分别是的中点,若.求证:(1)∥平面; (2)平面.备 注第 4 页共 4 页