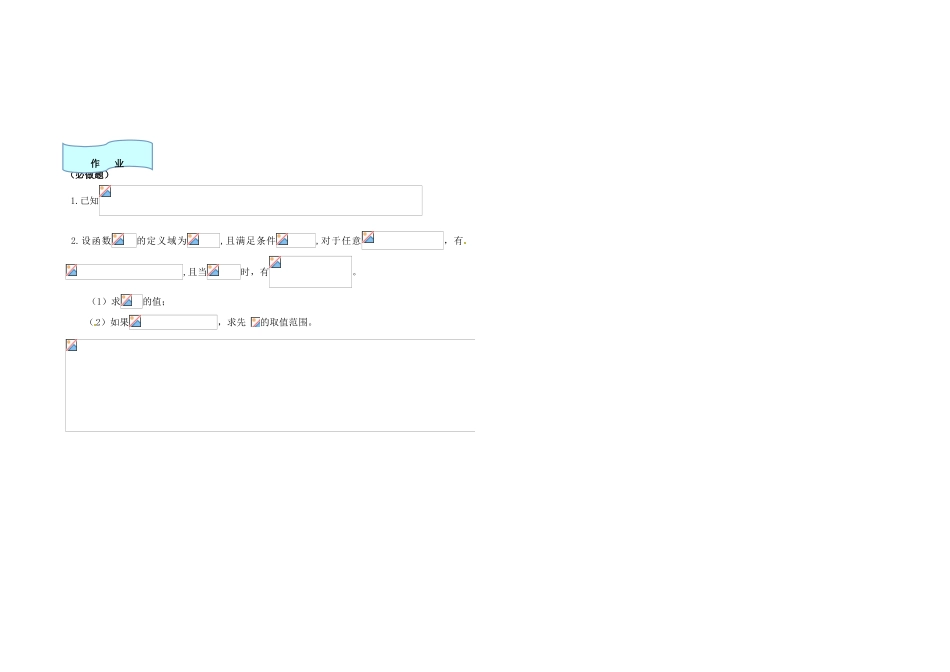
河南省郑州市实验高级中学高中数学 1.3 函数的单调性 2 学案 新人教 A版必修 11. 学会判断复合函数单调性;2. 会求解含有字母参数的问题;3. 会利用函数的单调性解不等式。 1.复合函数单调性增增增减减增减减 2.一般地,对于复合函数,如果在上是单调函数,并且在在 ,那么上的单调性可以简记为2.判断复合函数的单调性,要特别注意在 内研究。3.函数的单调递增区间是 例 1.已知函数,试求。(学习目标 1)变式:讨论函数的单调性。(学习目标 1)例 2.在(学习目标 2)变式:(学习目标 1)例 3.定义在上的函数,满足, 且当时,.(学习目标 3)(1)求的值.(2)求证:(3)求证:在上增函数; 自 主 探 究 交 流 探 究 标(4)若(5)比较变式:已知=,=1,解不等式:(学习目标 3)1.复合函数的单调性必须在共同的定义域内研究。2.已知函数的单调区间求参变量的取值范围,可根据函数单调性的证明方法,列出关于参数的不等式。3.解 决抽象函数相关题型,常常采用赋值法。 1.已知函数在区间[a,b]上单调,且,则方程在区间[a,b]内( )A.至少有一实根 B.至多有一实根 C.没有实根 D.必有唯一的实根2.已知函数,如果,那么函数( ) A.在区间(-1,0)上是减函数 B.在区间(0,1)上是减函数 C.在区间(-2,0)上是增函数 D.在区间(0,2)上是增函数3.已知函数 f(x)是 R 上的增函数,A(0,-1)、B(3,1)是其图象上的两点,那么不等式||<1 的解集的补集是( ) A.(-1,2) B.(1,4) C.(-∞,-1)∪[4,+∞) D . ( - ∞ , - 1)∪[2 , +∞)4.已知在区间(-∞,+∞)上是增函数,a、b∈R 且 a+b≤0,则下列不等式中正确的是( )A.(a)+(b)≤-(a)+(b)B.(a)+(b)≤(-a)+(-b)C.(a)+(b)≥-(a)+(b)D.(a)+b)≥(-a)+(-b)5.. 函 数在 [2 , + ∞ ] 上 递 减 , 则 a 的 取 值 范 围 是 __ .6.已知7.已知函数对任意的,都有,并且当时,(1)(2)若 归 类 方 法 自 主 测 评(必做题) 1.已知 2.设函数的定义域为,且满足条件,对于任意,有,且当时,有。 (1)求的值; (2)如果,求先 的取值范围。 作 业