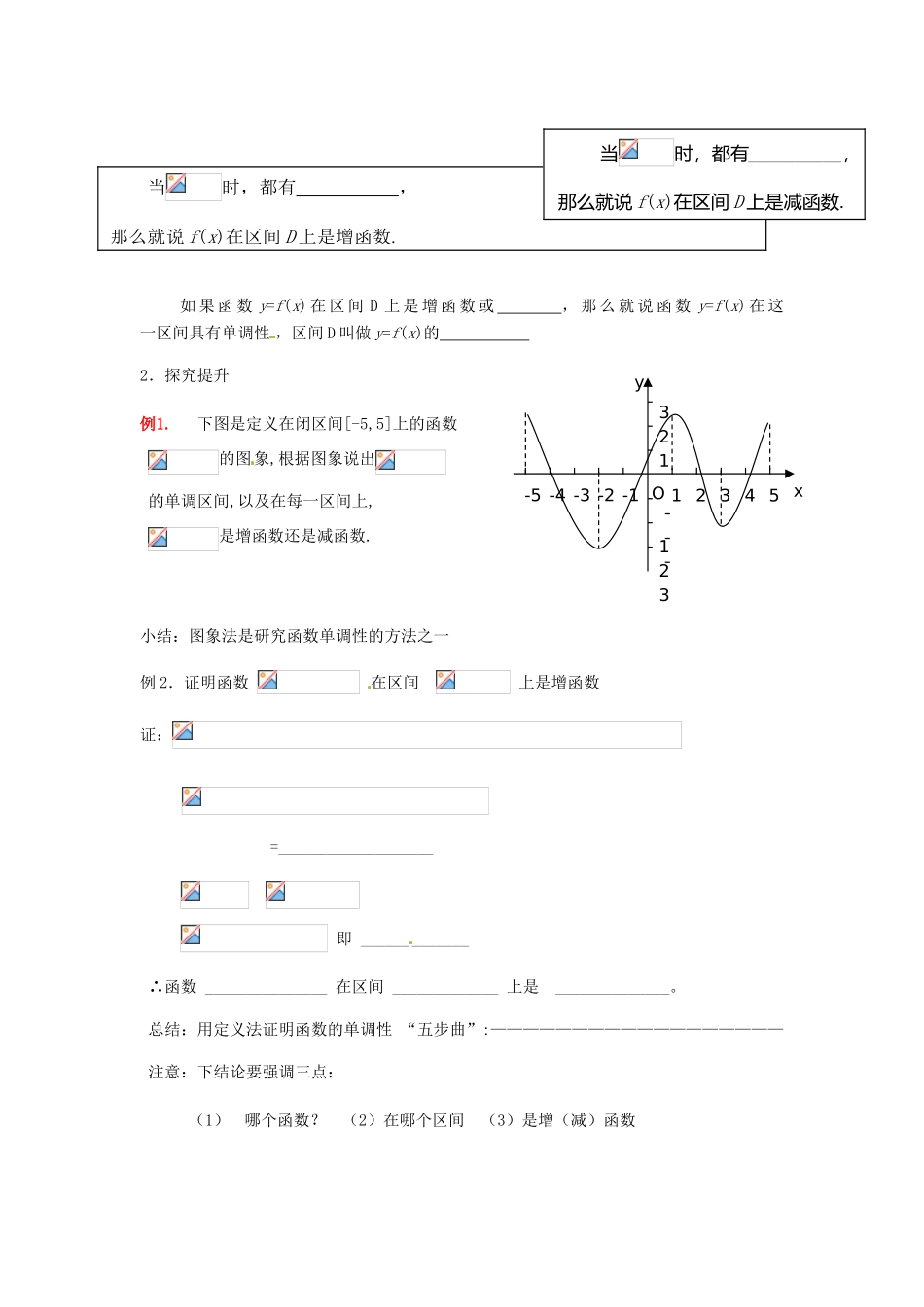
1、3、1 函数的单调性(1)一、预 案教材第 27~30 页,了解:(1)增函数和减函数的定义:① 图形语言 ② 符号语言(2)单调性和单调区间的定义:1.探索新知:观察函数,的图象从左至右看函数图象的变化规律:(1). 的图象是(上升)的,的图象在 y 轴左侧是______的,在 y 轴右侧是_______的.函数的单调性: 一般的,设函数 y=f(x)的定义域 为 I,如果对于定义域 I 内的某个区间 D上的任意两个自变量的值 x1,x2,xy0 x1 x2f(x1)f(x2)xy0x1 x2f(x1)f(x2)xy0xy0(2). 在上,f(x)随着 x 的增大而(增大);在 上,f(x)随着 x 的增大而_______;在上,f(x)随着 x 的增大而________.如 果 函 数 y=f(x) 在 区 间 D 上 是 增 函 数 或 , 那 么 就 说 函 数 y=f(x) 在 这 一区间具有单调性 ,区间 D 叫做 y=f(x)的 2.探究提升例1.下图是定义在闭区间[-5,5]上的函数 的图象,根据图象说出 的单调区间,以及在每一区间上, 是增函数还是减函数.小结:图象法是研究函数单调性的方法之一例 2.证明函数 在区间 上是增函数证: =___________________ 即 ______ _______∴函数 _______________ 在区间 _____________ 上是 ______________。总结:用定义法证明函数的单调性 “五步曲”:——————————————————注意:下结论要强调三点:(1)哪个函数? (2)在哪个区间 (3)是增(减)函数当时,都有 ,那么就说 f(x)在区间 D 上是增函数. 当时,都有__________,那么就说 f(x)在区间 D 上是减函数. xy1 2 3 4 5-2-4-1-3-5123-1-2-3O四、当堂检测:1、判断函数 在 是增函数还是减函数?证明你的结论。2、 判断函数在(0,+∞)上是增函数还是减函数?并给予证明。判断函数单调性的方法步骤利用定义证明函数 f(x)在给定 的区间 D 上的单调性的一般步骤: 取 值 → 作 差 → 变 形 → 定 号 → 下结论五.课后作 业1.函数在上单调递减,则的取值范围是( )A.k>0 B.k<0 C.k>-1 D.k<- 12.已知函数在(-2,3)上是减函数,则有( )A. f(-1)