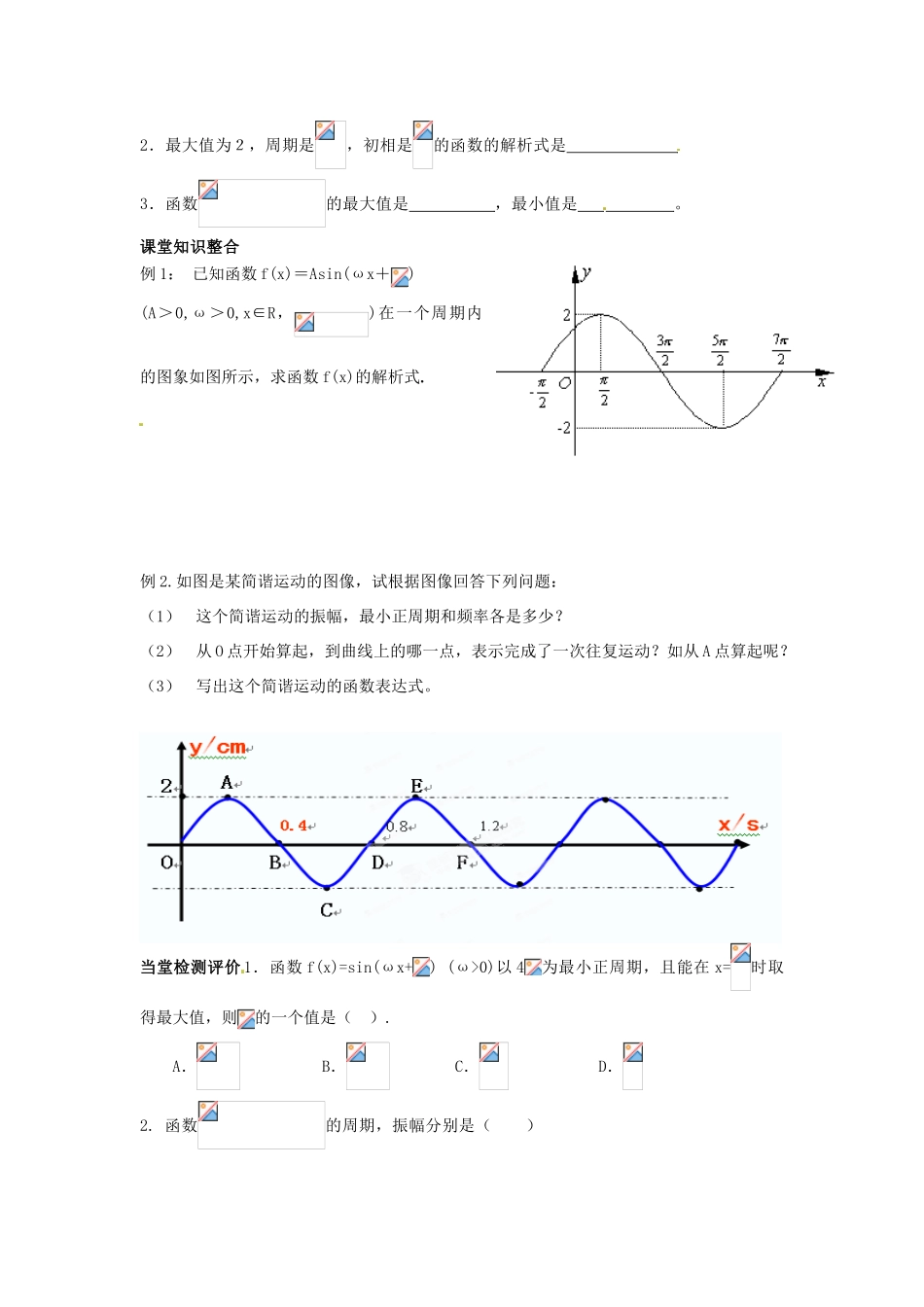
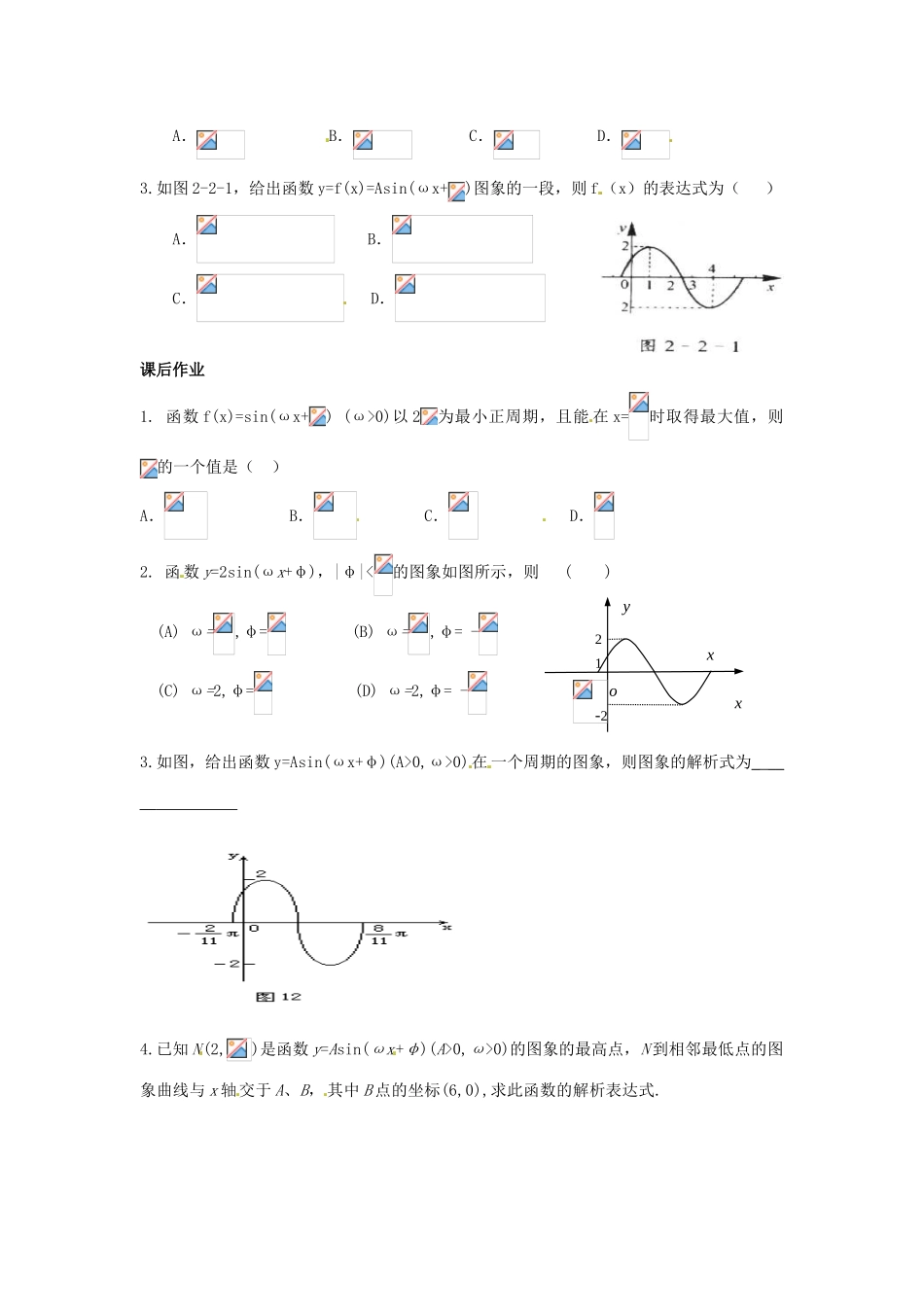
1.6 三角函数的应用学习目标:理解三角函数模型的简单问题,初步了解三角函数模型的简单应用(1)函数 y=Asin(ωx+φ) (A>0,ω>0)中常数的物理意义,理解振幅,周期,频率,相位,初相。( 2 ) 熟 练 函 数 y=Asin(ωx+φ) ( A>0,ω>0 ) 的 有 关 性 质 , 学 会 由 图 像 求 解 析 式y=Asin(ωx+φ).例 2:画出函数的图象并观察其周期.3. 变式:作出函数 y=|cos x|,x∈R 的图象,判断它的奇偶性并写出其周期和单调区间对于小组合作交流1.函数的周期,振幅分别是( )A. B. C. D.2.最大值为2,周期是,初相是的函数的解析式是 3.函数的最大值是 ,最小值是 。课堂知识整合例 1: 已知函数 f(x)=Asin(ωx+)(A>0,ω>0,x∈R,)在一个周期内的图象如图所示,求函数 f(x)的解析式.例 2.如图是某简谐运动的图像,试根据图像回答下列问题:(1)这个简谐运动的振幅,最小正周期和频率各是多少?(2)从 O 点开始算起,到曲线上的哪一点,表示完成了一次往复运动?如从 A 点算起呢?(3)写出这个简谐运动的函数表达式。当堂检测评价 1.函数 f(x)=sin(ωx+) (ω>0)以 4为最小正周期,且能在 x=时取得最大值,则的一个值是( ).A. B. C. D.2. 函数的周期,振幅分别是( )A. B. C. D.3.如图 2-2-1,给出函数 y=f(x)=Asin(ωx+)图象的一段,则 f (x)的表达式为( )A. B.C. D.课后作业1. 函数 f(x)=sin(ωx+) (ω>0)以 2为最小正周期,且能 在 x=时取得最大值,则的一个值是( )A. B. C. D.2. 函 数 y=2sin(ωx+φ),|φ|<的图象如图所示,则 ( )(A) ω=,φ= (B) ω=,φ= -(C) ω=2,φ= (D) ω=2,φ= -3.如图,给出函数 y=Asin(ωx+φ)(A>0,ω>0)在 一个周期的图象,则图象的解析式为_ __ __ 4.已知 N(2,)是函数 y=Asin(ωx+φ)(A>0,ω>0)的图象的最高点,N 到相邻最低点的图象曲线与 x 轴交于 A、B, 其中 B 点的坐标(6,0),求此函数的解析表达式.xy12o-2x5.如图表示电流 I 与时间 t 的函数关系式: I =在同一周期内的图象。(1)根据图象写出 I =的解析式;(2)为了使 I =中 t 在任意-段秒的时间内电流 I 能同时取得最大值和最小值,那么正整数的最小值是多少?