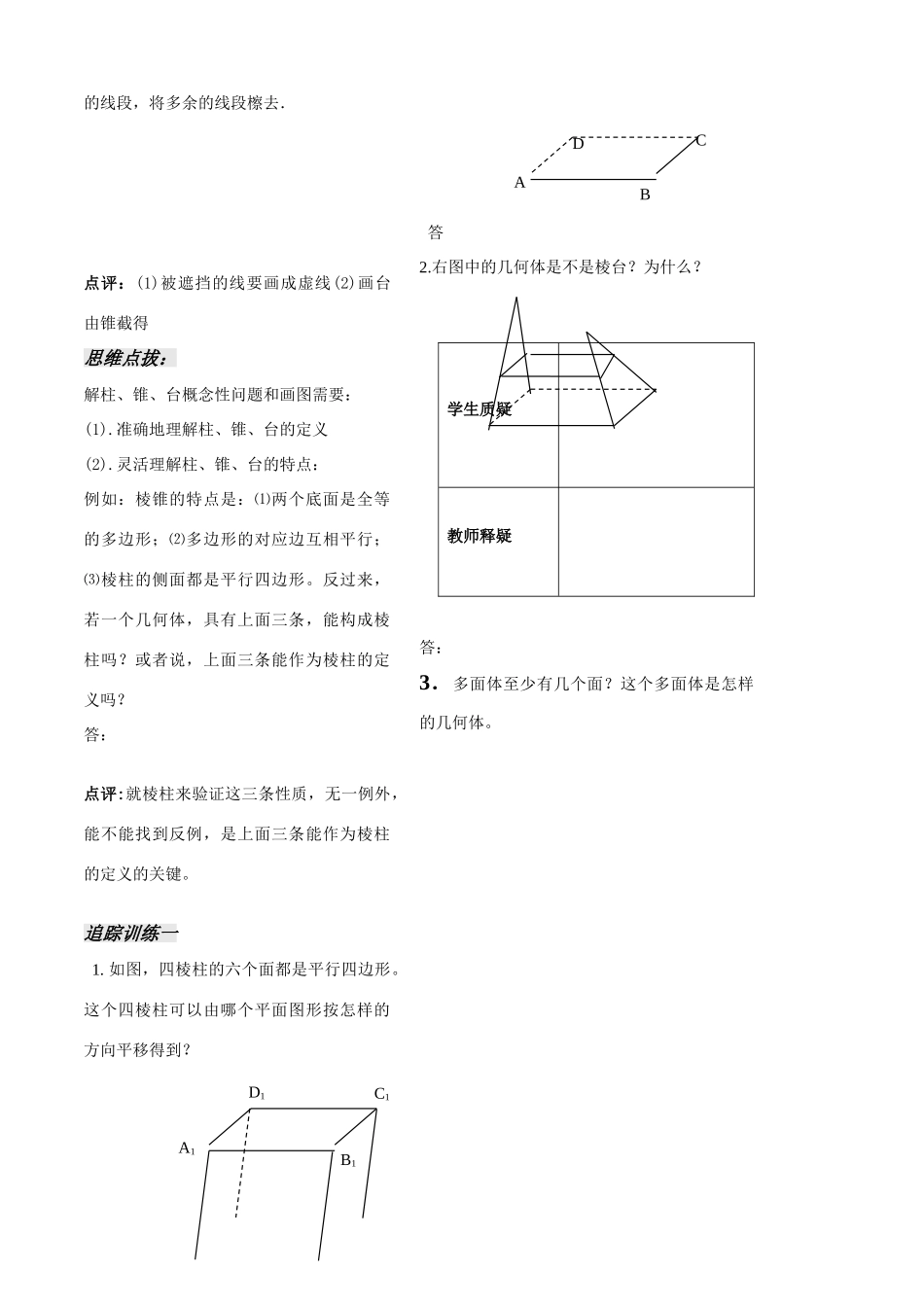
第一章 立体几何初步一、知识结构二、重点难点重点:空间直线,平面的位置关系。柱、锥、台、球的表面积和体积的计算公式。平行、垂直的定义,判定和性质。难点:柱、锥、台、球的结构特征的概括。文字语言,图形语言和符号语言的转化。平行,垂直判定与性质定理证明与应用。空间几何体简单的空间几何体基本元素 ( 点、线、面 ) 关系多面体 ( 棱柱、棱锥、棱台 )旋转体(圆柱、圆锥、圆台)直 线 与直线直 线 与平面平面与平面结构特征,图形表示,侧面积,体积平行、垂直、夹角、距离三视图,直观图,展开图判定、性质综合应用听课随笔第一课时 棱柱、棱锥、棱台 【学习导航】 知识网络 学习要求 1.初步理解棱柱、棱锥、棱台的概念。掌握它们的形成特点。 2.了解棱柱、棱锥、棱台中一些常用名称的含义。 3.了解棱柱、棱锥、棱台这几种几何体简单作图方法4.了解多面体的概念和分类.自学评价1. 棱柱的概念: 表示法:思考:棱柱的特点:.【答】 2. 棱锥的概念: 表示法:思考:棱锥的特点:.【答】 3.棱台的概念: 表示法:思考:棱台的特点:.【答】 4.多面体的概念: 5.多面体的分类:⑴ 棱柱的分类 ⑵ 棱锥的分类 ⑶ 棱台的分类 【精典范例】例 1:设有三个命题:甲:有两个面平行,其余各面都是平行四边形所围体一定是棱柱;乙:有一个面是四边形,其余各面都三角形所围成的几何体是棱锥;丙:用一个平行与棱锥底面的平面去截棱锥,得到的几何体叫棱台。 以上各命题中,真命题的个数是 ( )A.0 B. 1 C. 2 D. 3例 2:画一个四棱柱和一个三棱台。【解】四棱柱的作法:⑴ 画上四棱柱的底面----画一个四边形;⑵ 画侧棱-----从四边形的每一个顶点画平行且相等的线段;⑶ 画下底面------顺次连结这些线段的另一个端点⑷ 画一个三棱锥,在它的一条侧棱上取一点,从这点开始,顺次在各个侧面画出与底面平行听课随笔棱柱、棱锥、棱台棱柱的结构特征棱锥的结构特征棱台的结构特征的线段,将多余的线段檫去.点评:(1)被遮挡的线要画成虚线(2)画台由锥截得思维点拔:解柱、锥、台概念性问题和画图需要:(1).准确地理解柱、锥、台的定义(2).灵活理解柱、锥、台的特点:例如:棱锥的特点是:⑴两个底面是全等的多边形;⑵多边形的对应边互相平行;⑶棱柱的侧面都是平行四边形。反过来,若一个几何体,具有上面三条,能构成棱柱吗?或者说,上面三条能作为棱柱的定义吗?答:点评:就棱柱来验证这...