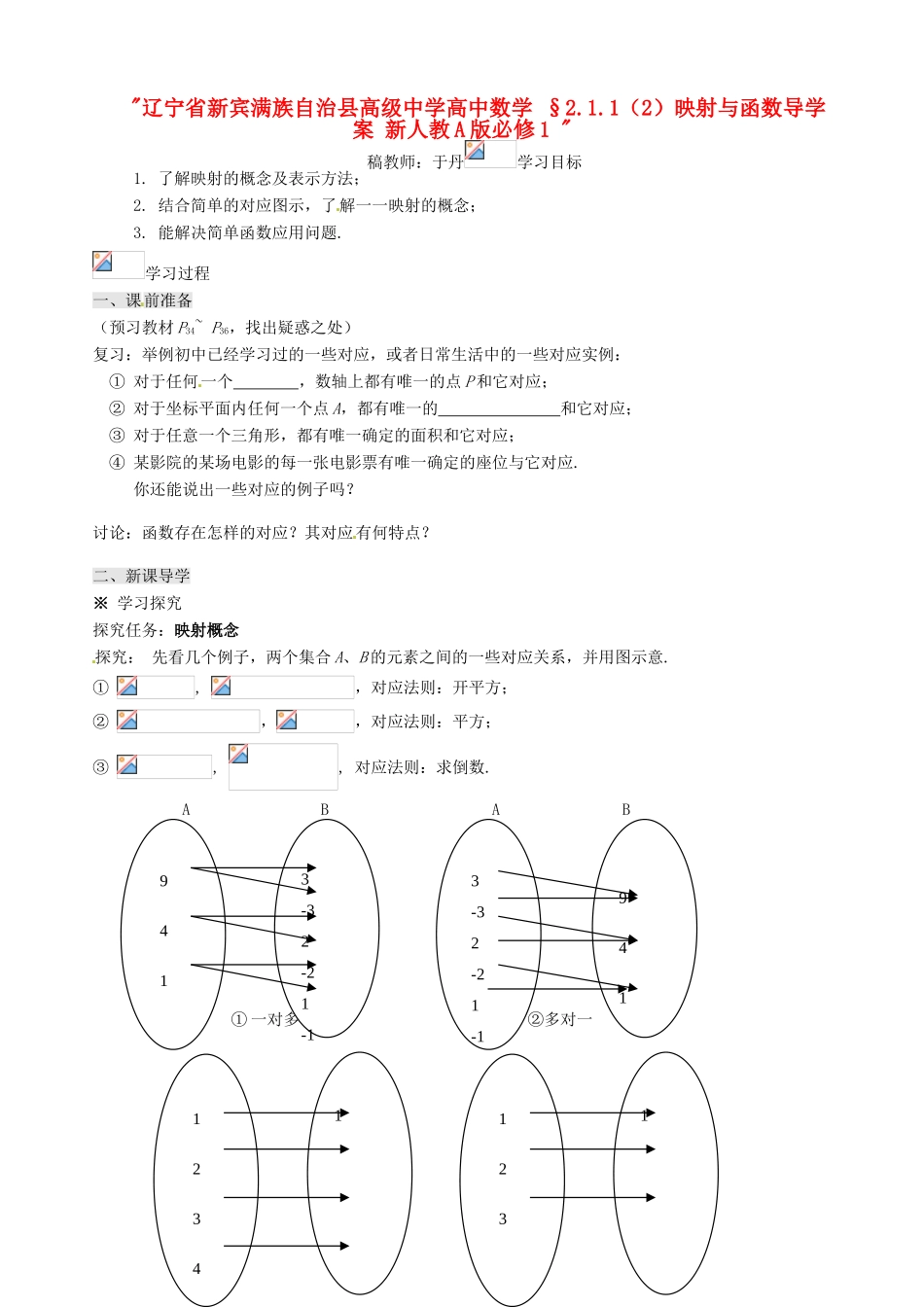
"辽宁省新宾满族自治县高级中学高中数学 §2.1.1(2)映射与函数导学案 新人教 A 版必修 1 "稿教师:于丹学习目标1. 了解映射的概念及表示方法;2. 结合简单的对应图示,了解一一映射的概念;3. 能解决简单函数应用问题.学习过程一、课前准备(预习教材 P34~ P36,找出疑惑之处)复习:举例初中已经学习过的一些对应,或者日常生活中的一些对应实例:① 对于任何一个 ,数轴上都有唯一的点 P 和它对应;② 对于坐标平面内任何一个点 A,都有唯一的 和它对应;③ 对于任意一个三角形,都有唯一确定的面积和它对应;④ 某影院的某场电影的每一张电影票有唯一确定的座位与它对应. 你还能说出一些对应的例子吗?讨论:函数存在怎样的对应?其对应有何特点?二、新课导学※ 学习探究探究任务:映射概念探究: 先看几个例子,两个集合 A、B 的元素之间的一些对应关系,并用图示意.① , ,对应法则:开平方;② ,,对应法则:平方;③ , , 对应法则:求倒数. A B A B① 一对多 ②多对一 A B A B 3 -3 2 -2 1 -1941 1 2 3 1 1 2 3 41 9 4 13-32-21-1 新知:一般地,设 A、B 是两个非空集合,如果按照某种对应法则 f,对集合 A 中的任意一个元素 x,在集合 B 中都有一个且仅有一个元素 y 与之对应,那么就称对 应为从集合 A 到集合 B 的一个映射(mapping).记作“”。这时,称 y 是 x 在映射 f 的作用下的象。 记作,于是,称做的原象。其中A 叫做映射的 (函数定义域的推广),由所有象构成的集合叫做映射 的 ,通常记作 一一映射: ※ 典型例题例 1、设集合 A={a,b,c}, B ={x,y,z},从集合 A 到集合 B 的对应方式如下图所示,其中,哪几个对应关系是从集合 A 到集合 B 的映射?A B A B A B A B A B① ② ③ ④ ⑤ 例 2、判断下列对应哪些是由 A 到 B 的映射?为什么?(1)A=R,;(2)A=R,;(3) (4)A=Z,B=Q, 学习评价 ※ 当堂检测③ 一对一④ 一对一余abcxyzabcxyzabcxyzabcxyzabcxyz1. 在映射中,,且,则与 A 中的元素 对应的 B 中的元素为( ).A.B. C.D.2.下列对应:① ②③不是从集合 A 到 B 映射的有( ). A. ①②③ B. ①② C. ②③ D. ①③3.设集合 A={2, 4, 6, 8, 10}, B={1, 9, 25, 49, 81, 100},下面的对应关系能构成 A 到 B 的映射的是( ) A、B、 C、D、4.已知集合从集合 A 到集合 B 的映射,试问能构造出多少映射?