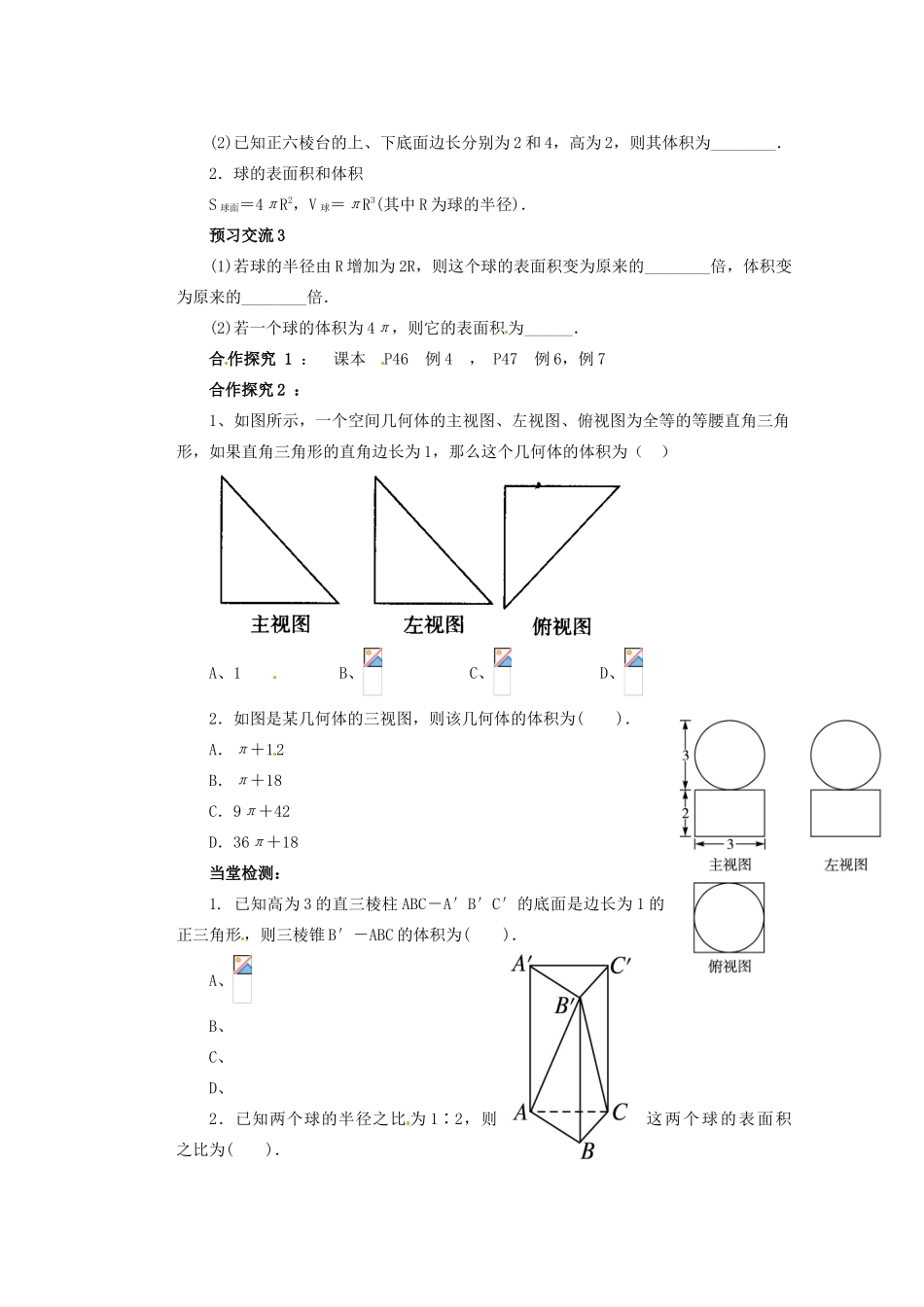
陕西省澄城县寺前中学高一数学教学案:简单几何体的体积学习目标1.在上一节学习的基础上,会用公式求柱、锥、台体的体积.了解柱、锥、台体的体积之间的关系.2.记住球的表面积和体积公式,并进行有关计算.学习重点柱体、锥体、台体的体积的计算.会用公式求球的表面积和体积.学习难点与球有关的组合体的体积计算.阅读课本 P45---P48,认真完成学案:1.柱、锥、台体的体积V 柱体=Sh(S 为柱体的底面积,h 为柱体的高).V 锥体=Sh(S 为锥体的底面积,h 为锥体的高).V 台体=(S 上+S 下+)h(S 上,S 下分别为棱台的上,下底面积,h 为高).预习交流 1柱体、锥体、台体的体积公式有何联系?提 示:台体的体积公式中,如果设 S 上=S 下,就得到柱体的体积公式 V 柱体=Sh;如果设 S 上=0,就得到锥体 的体积公式 V 锥体=Sh.因此,柱体、锥体、台体的体积公式之间的关系,可表示如下.由上可见,柱体、锥体的体积公式是台体的体积公式的特例.预习交流 2(1)正棱锥的高和底面边长都缩小为原来的,则它的体积是原来的( ).A、 B、C、 D、(2)已知正六棱台的上、下底面边长分别为 2 和 4,高为 2,则其体积为________.2.球的表面积和体积S 球面=4πR2,V 球=πR3(其中 R 为球的半径).预习交流 3(1)若球的半径由 R 增加为 2R,则这个球的表面积变为原来的________倍,体积变为原来的________倍.(2)若一个球的体积为 4π,则它的表面积为______.合作探究 1 : 课本 P46 例 4 , P47 例 6,例 7合作探究 2 : 1、如图所示,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为 1,那么这个几何体的体积为( )A、1B、C、D、2.如图是某几何体的三视图,则该几何体的体积为( ).A.π+12 B.π+18C.9π+42 D.36π+18当堂检测:1. 已知高为 3 的直三棱柱 ABC-A′B′C′的底面是边长为 1 的正三角形,则三棱锥 B′-ABC 的体积为( ).A、 B、C、 D、2.已知两个球的半径之比 为 1∶2,则这两个球的表面积之比为( ).A.1∶2 B.1∶4C.1∶6 D.1∶83.圆台的上、下 底面的面积分别为 π,4π,侧面积是 6π,这个圆台的体积是( ).A、B、2πC、 D、