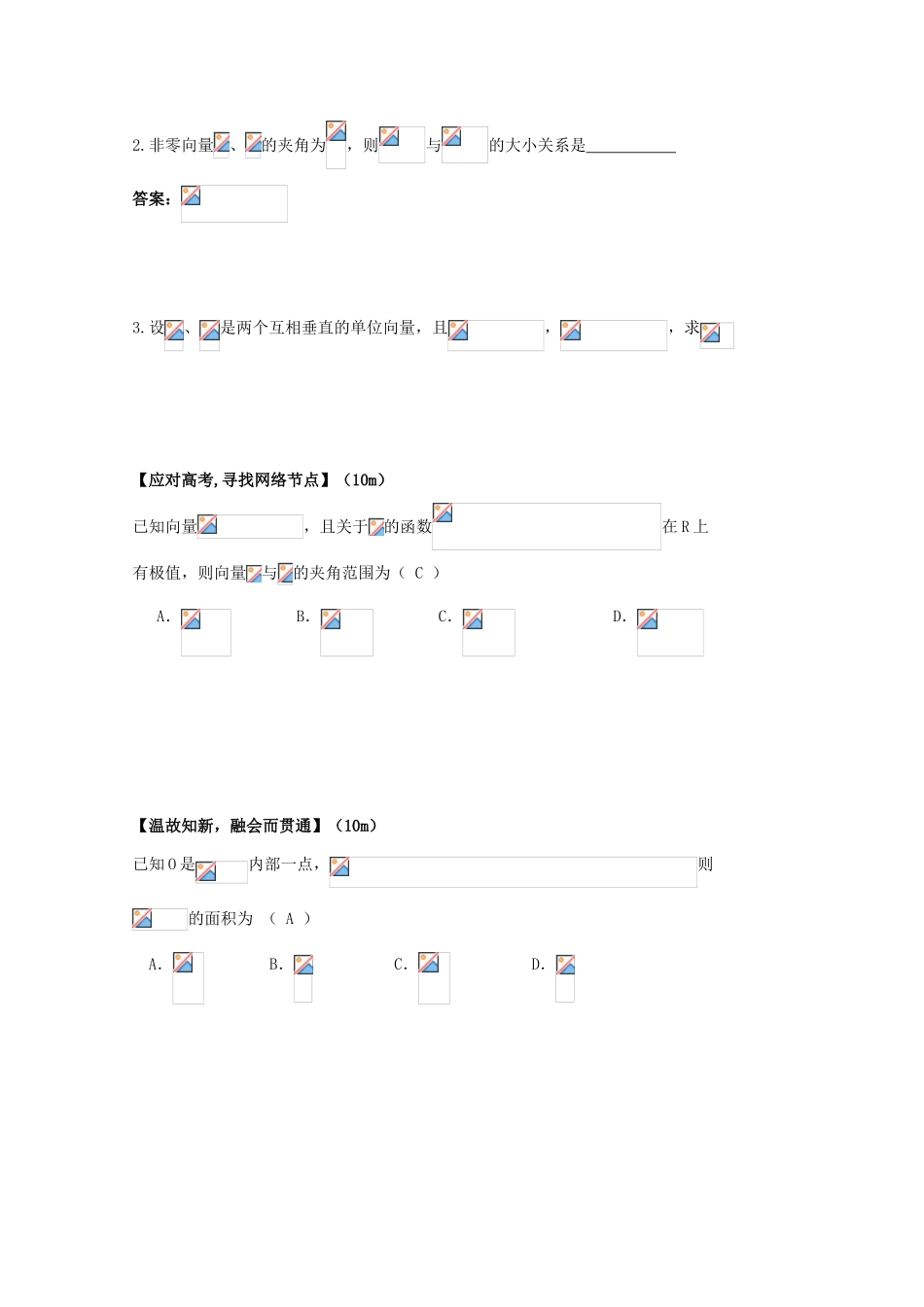
学案 49 平面向量的概念与几何运算(1)【课前预习,听课有针对性】(5m)1.判断题:①若为单位向量,则.( )②若,则∥.( )2.与=(3,-4)平行的单位向量是_________;【及时巩固,牢固掌握知识】(20——30m)A 组 夯实基础,运用知识1.如图所示,向量,A、B、C 在一条直线上,且,则( )A. B.C. D.2.已知,在方向上的投影是,则是( )A.3 B. C.2 D.3.如图:梯形 ABCD 中,AB//CD,且 AB=2CD,M、N 是 DC、BA 的中点,设,,ACBODNMCBA试以、为基底表示、。4.下列说法不正确的是( )(A) (B) (C) (D)5.如图,O 为正六边形 ABCDEF 的中心,则向量、、、中,共线的向量共有( )对(A)0 (B)1 (C)2 (D)3 6.在中,AB=7,BC=5,AC=6,则等于( )(A) (B)38 (C) (D)19 B 组 提高能力,灵活迁移1.在所在平面内有一点 P,使得,则点 P 一定是的( B )(A)重心 (B)垂心 (C)内心 (D)外心2.非零向量、的夹角为,则与的大小关系是 答案:3.设、是两个互相垂直的单位向量,且,,求【应对高考,寻找网络节点】(10m)已知向量,且关于的函数在 R 上有极值,则向量与的夹角范围为( C )A. B. C. D.【温故知新,融会而贯通】(10m)已知 O 是内部一点,则的面积为 ( A )A. B. C. D.向量=(),是直线 y=x 的方向向量,a =5,则数列的前 10 项的和( A )A.50 B.100 C.150 D.200