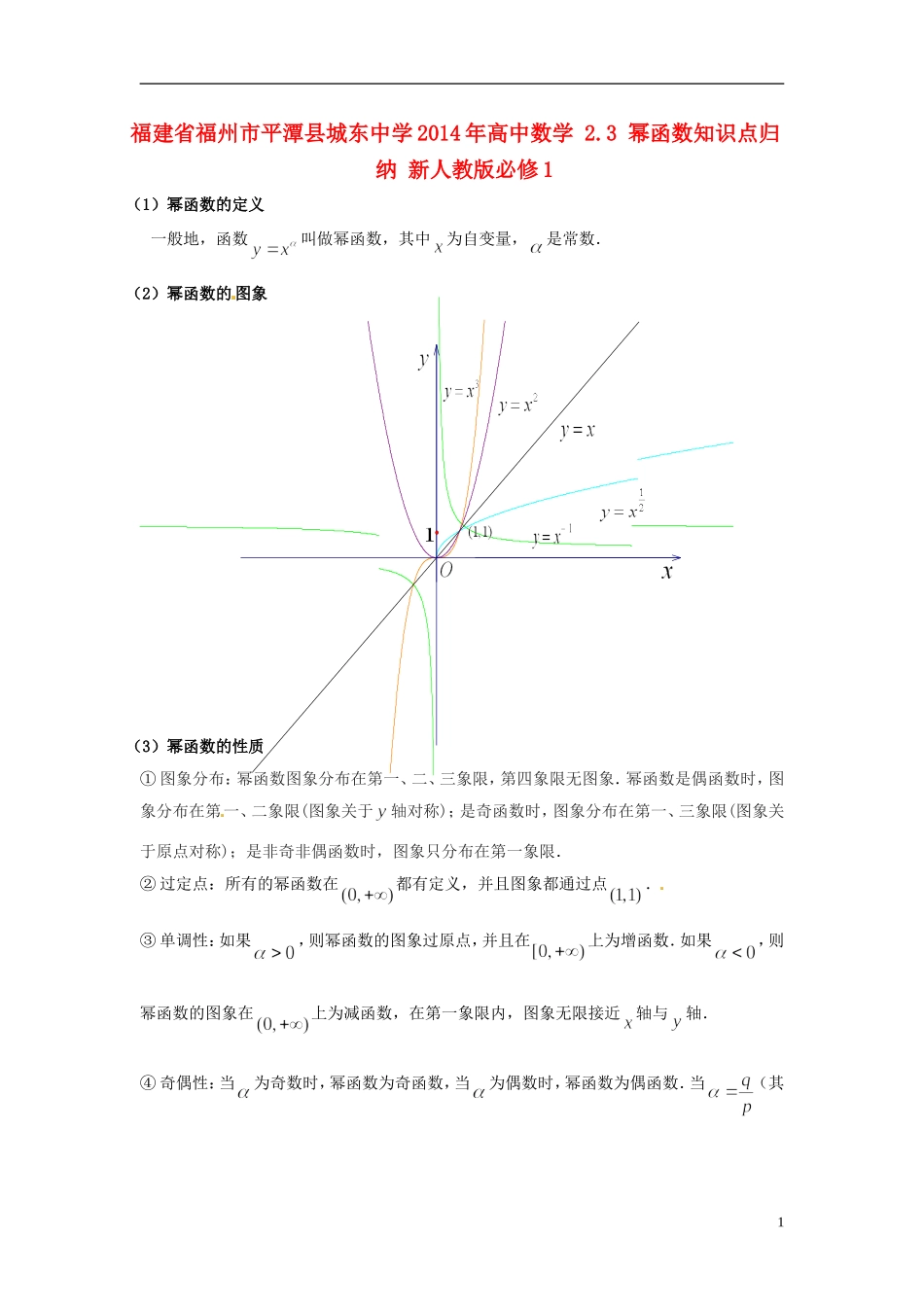
福建省福州市平潭县城东中学 2014 年高中数学 2.3 幂函数知识点归纳 新人教版必修 1(1)幂函数的定义 一般地,函数叫做幂函数,其中为自变量,是常数.(2)幂函数的 图象(3)幂函数的性质① 图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限. ② 过定点:所有的幂函数在都有定义,并且图象都通过点. ③ 单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.④ 奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当(其1中互 质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则是偶函数,若为偶数为奇数时,则是非奇非偶函数.⑤ 图象特征:幂函数,当时,若,其图象在直线下方,若,其图象在直线上方,当时,若,其图象在直线上方,若,其图象在直线下方.〖补充知识〗二次函数(1)二次函数解析式的三种形式① 一般式:②顶点式:③两根式:(2)求二次函数解析式的方法① 已知三个点坐标时,宜用一般式.② 已知抛物线的顶点坐标或与 对称轴有关或与最大(小)值有关时,常使用顶点式.③ 若已知抛物线与轴有两个交点,且横线坐标已知时,选用两根式求更方便.(3)二次函数图象的性质① 二次函数的图象是一条抛物线,对称轴方程为顶点坐标是.② 当时,抛物线开口向上,函数在上递减,在上递增,当时,;当时,抛物线开口向下,函数在上递增,2在上递减,当时,.③ 二次函数当时,图象与轴有两个交点.(4)一元二次方程根的分布一元 二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的 判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布. 设一元二次方程的两实根为,且.令,从以下四个方面来分析此类问题:①开口方向: ②对称轴位置: ③判别式: ④端点函数值符号. ①k<x1≤x2 ②x1≤x2<k 3 ③x1<k<x2 af(k)<0 ④k1<x1≤x2<k2 ⑤ 有且仅有一个根 x1(或 x2)满足 k1<x1(或 x2)<k2 f(k1)f(k2)0,并同时考虑 f(k 1)=0 或 f(k2)=0 这两种情况...