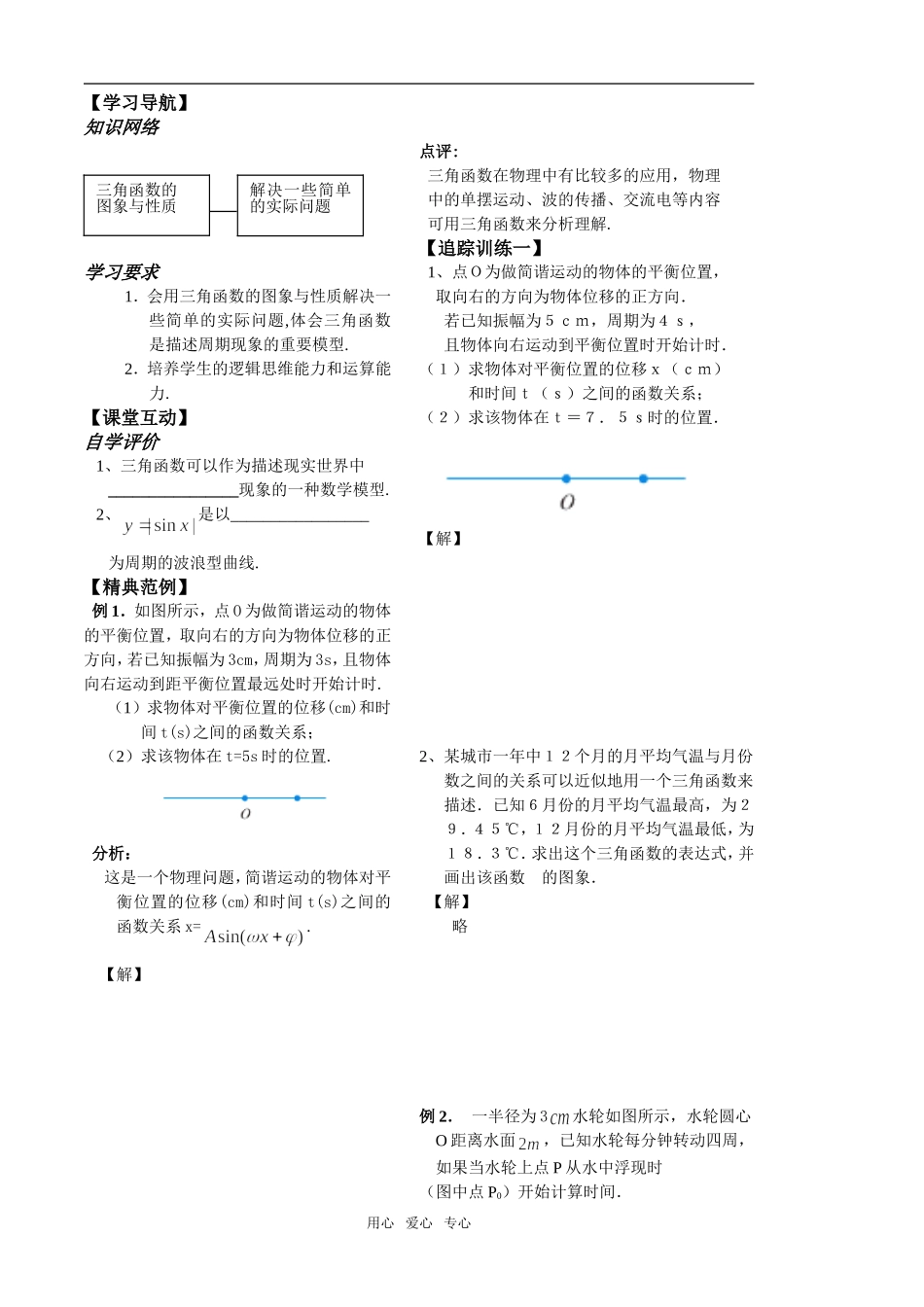
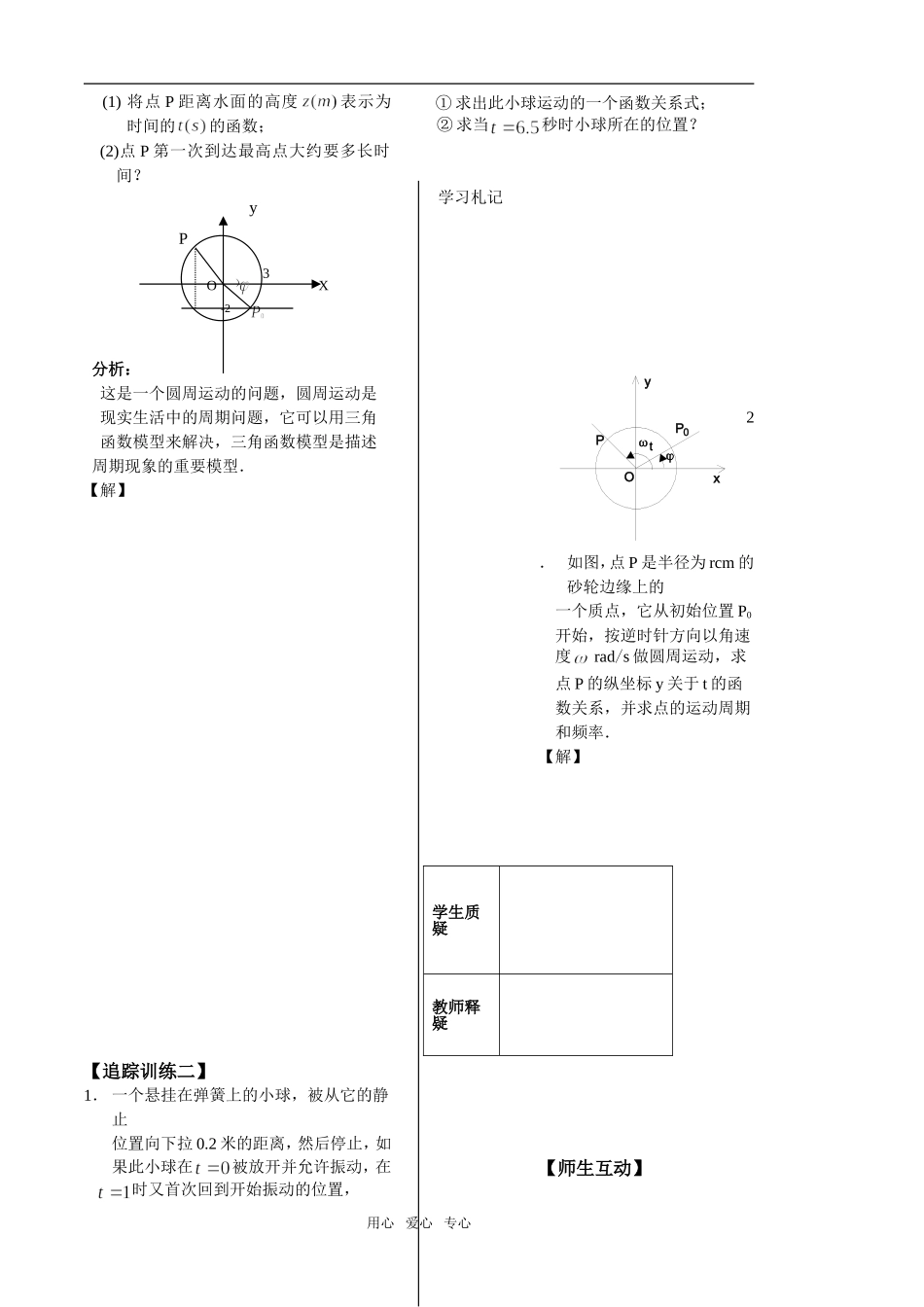
第 8 课时 用心 爱心 专心学习札记【学习导航】 知识网络 学习要求 1.会用三角函数的图象与性质解决一些简单的实际问题,体会三角函数是描述周期现象的重要模型.2.培养学生的逻辑思维能力和运算能力.【课堂互动】自学评价 1、三角函数可以作为描述现实世界中 ________________现象的一种数学模型. 2、是以_________________ 为周期的波浪型曲线.【精典范例】例 1.如图所示,点 O 为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为 3cm,周期为 3s,且物体向右运动到距平衡位置最远处时开始计时.(1)求物体对平衡位置的位移(cm)和时间 t(s)之间的函数关系; (2)求该物体在 t=5s 时的位置.分析: 这是一个物理问题,简谐运动的物体对平衡位置的位移(cm)和时间 t(s)之间的函数关系 x=.【解】 点评: 三角函数在物理中有比较多的应用,物理中的单摆运动、波的传播、交流电等内容可用三角函数来分析理解.【追踪训练一】1、点O为做简谐运动的物体的平衡位置, 取向右的方向为物体位移的正方向.若已知振幅为5cm,周期为4s,且物体向右运动到平衡位置时开始计时.(1)求物体对平衡位置的位移x(cm) 和时间t(s)之间的函数关系;(2)求该物体在t=7.5s时的位置.【解】2、某城市一年中12个月的月平均气温与月份数之间的关系可以近似地用一个三角函数来描述.已知6月份的月平均气温最高,为29.45℃,12月份的月平均气温最低,为18.3℃.求出这个三角函数的表达式,并画出该函数 的图象.【解】略例 2. 一半径为 3水轮如图所示,水轮圆心O 距离水面,已知水轮每分钟转动四周,如果当水轮上点 P 从水中浮现时(图中点 P0)开始计算时间.用心 爱心 专心三角函数的图象与性质解决一些简单的实际问题(1) 将点 P 距离水面的高度表示为时间的的函数;(2)点 P 第一次到达最高点大约要多长时间?分析: 这是一个圆周运动的问题,圆周运动是 现实生活中的周期问题,它可以用三角 函数模型来解决,三角函数模型是描述 周期现象的重要模型.【解】 【追踪训练二】1. 一个悬挂在弹簧上的小球,被从它的静止位置向下拉 0.2 米的距离,然后停止,如果此小球在被放开并允许振动,在 时又首次回到开始振动的位置,① 求出此小球运动的一个函数关系式;② 求当秒时小球所在的位置?2. 如图,点 P 是半径为 rcm 的砂轮边缘上的一个质点,...