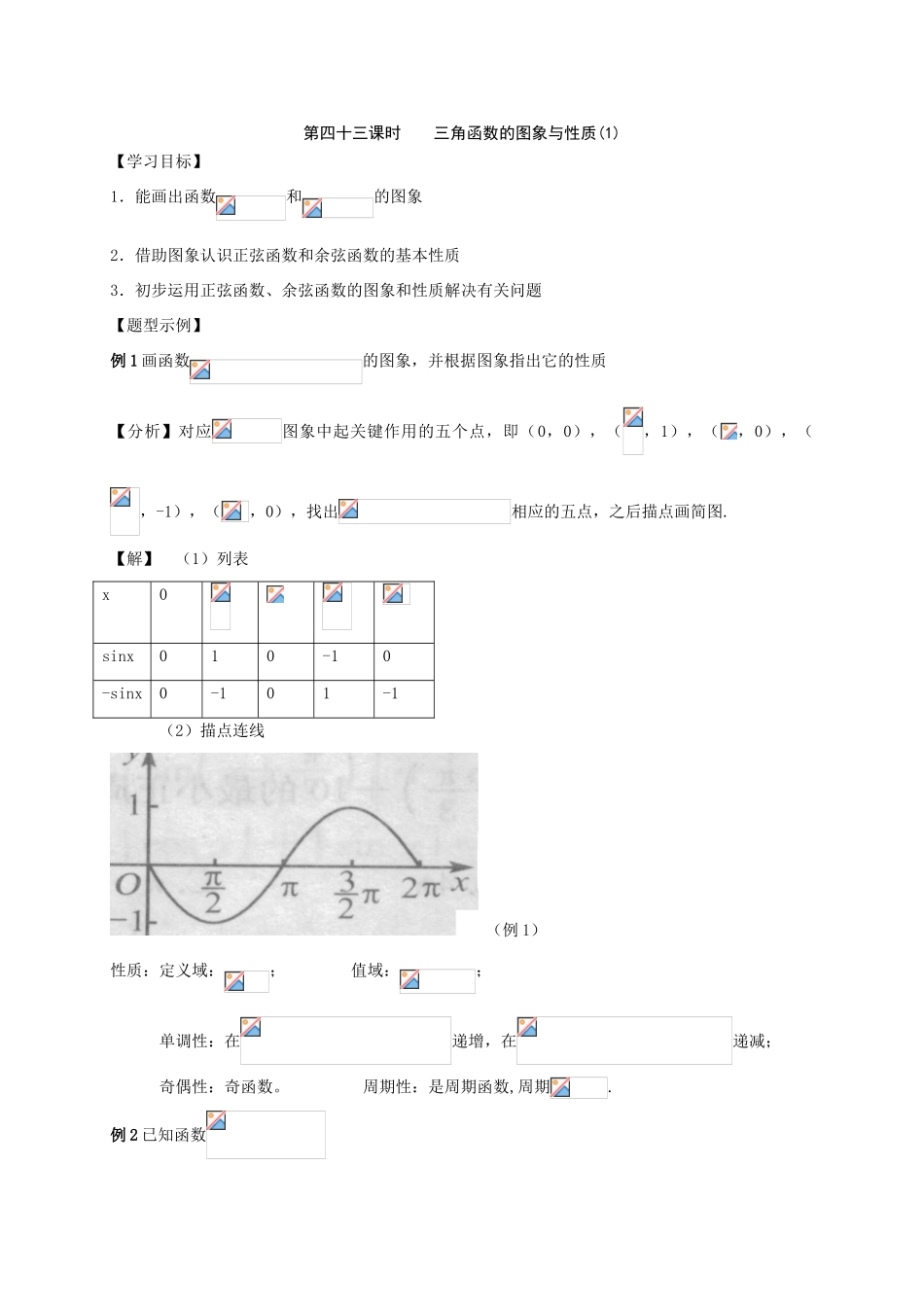
第四十三课时 三角函数的图象与性质(1)【学习目标】1.能画出函数和的图象2.借助图象认识正弦函数和余弦函数的基本性质3.初步运用正弦函数、余弦函数的图象和性质解决有关问题【题型示例】例 1 画函数的图象,并根据图象指出它的性质【分析】对应图象中起关键作用的五个点,即(0,0),(,1),(,0),(,-1),(,0),找出相应的五点,之后描点画简图.【解】 (1)列表 x0sinx010-10-sinx0-101-1(2)描点连线(例 1)性质:定义域:; 值域:; 单调性:在递增,在递减;奇偶性:奇函数。 周期性:是周期函数,周期.例 2 已知函数(1)求它的最大值及相应的 x 的值;(2)求它的单调减区间.【分析】依据的性质解决本题。把“”看作一个整体.【解】 (1)令=t,函数的最大值是 1,此时.所以的最大值为 1, 此时,即(2)函数的单调减区间是即,解得所以单调减区间为例 3 比较下列各组值的大小(1)与 (2)与【分析】利用诱导公式化到同一单调区间内进行比较.【解】 (1),,由在是减函数,所以,故(2),由在是增函数,所以。故【拓展创新】在内使成立的 x 的取值范围是 ( )A B C D 【分析】(解法一)在单位圆中用正弦线、余弦线比较即等 C (解法二)在同一坐标系内作出的图象,观察它们的位置关系,选 C (解法三)取,要满足,对照选项,排除后选 C【反思升华】1.画好、用好和的图象;2.能借助图象观察得到正弦函数、余弦函数的基本性质;3.注重数形结合、整体思想等思想方法在解题中的运用;4.感受从特殊到一般的研究问题的方法.【学习评价】1.函数的定义域为 ( )A. B. C. D. 2.函数的值域 ( )A. [-1,1] B. [,1] C. [,] D. [,1]3.下列函数在上为增函数是 ( ) A. B. C. D. 4.若是减函数,是增函数,那么角 x 在A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限5.观察函数的图象,它的一条对称轴为 ( )A. B. C. D. 6.函数的一个单调增区间是 ( )A. B. C.D.7.不求值比较大小 (1) ;(2) .8.函数的单调增区间为 .9.是奇函数,当 x>0 时,则当 x<0 时,= .10.函数的最小值为 ,相应的 x 的值是 .11.作函数的简图,并指出它的值域、单调区间.12.判断下列函数的奇偶性(1) (2)13.已知函数的最大值为 3,最小值为 1(1)求 a、b 的值;(2)求函数的单调增区间.