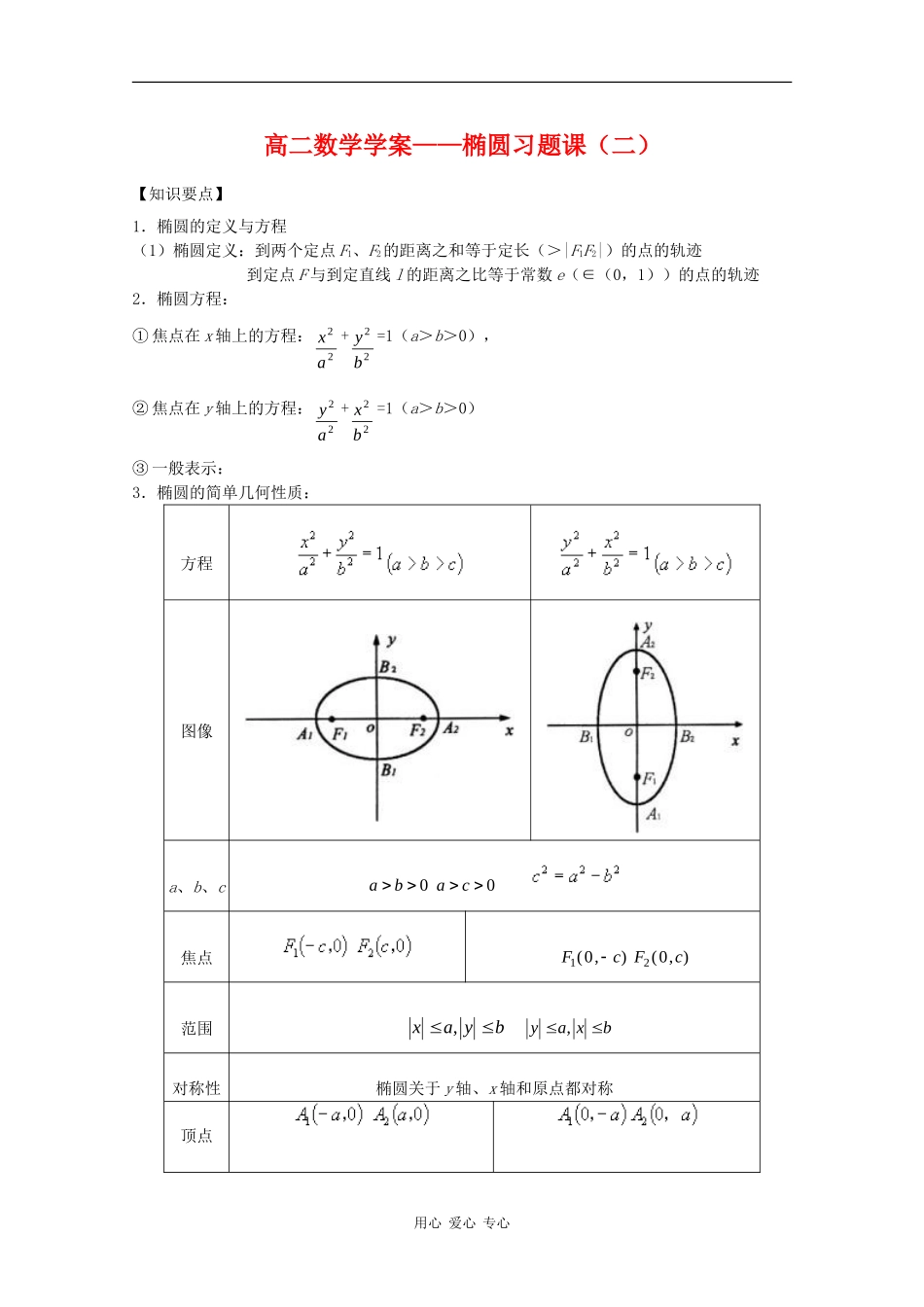
高二数学学案——椭圆习题课(二)【知识要点】1.椭圆的定义与方程(1)椭圆定义:到两个定点 F1、F2的距离之和等于定长(>|F1F2|)的点的轨迹到定点 F 与到定直线 l 的距离之比等于常数 e(∈(0,1))的点的轨迹2.椭圆方程:① 焦点在 x 轴上的方程:22ax+22by=1(a>b>0),② 焦点在 y 轴上的方程:22ay+22bx=1(a>b>0)③ 一般表示:3.椭圆的简单几何性质:方程图像a、b、c00caba 焦点 ),0(),0(21cFcF范围byax , bxay ,对称性椭圆关于 y 轴、x 轴和原点都对称顶点 用心 爱心 专心 长轴: A1A2 长轴长 短轴:B1B2短轴长 离心率【基础训练】1. 已知 F1、F2是两定点421FF动点 M 满足421 MFMF,则动点 M 的轨迹是A.椭圆 B 直线 C 圆 D 线段2.(2003 年北京宣武区模拟题)已知 F1、F2是椭圆162x+92y=1 的两个焦点,过 F1的直线与椭圆交于 M、N 两点,则△MNF2的周长为A.8 B.16 C.25 D.32解析:利用椭圆的定义易知 B 正确.答案:B3.(2004 年湖北,6)已知椭圆162x+92y=1 的左、右焦点分别为 F1、F2,点 P 在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点 P 到 x 轴的距离为A. 59 B.3 C.779 D. 49 解析:由余弦定理判断∠P<90°,只能∠PF1F2或∠PF2F1为直角.由 a=4,b=3 得 c=7 ,∴|yP|=49 .答案:D4.如果方程 x2+ky2=2 表示焦点在 y 轴的椭圆,那么实数 k 的取值范围是____________.解析:椭圆方程化为22x+ky22=1.焦点在 y 轴上,则k2 >2,即 k<1.又 k>0,∴0