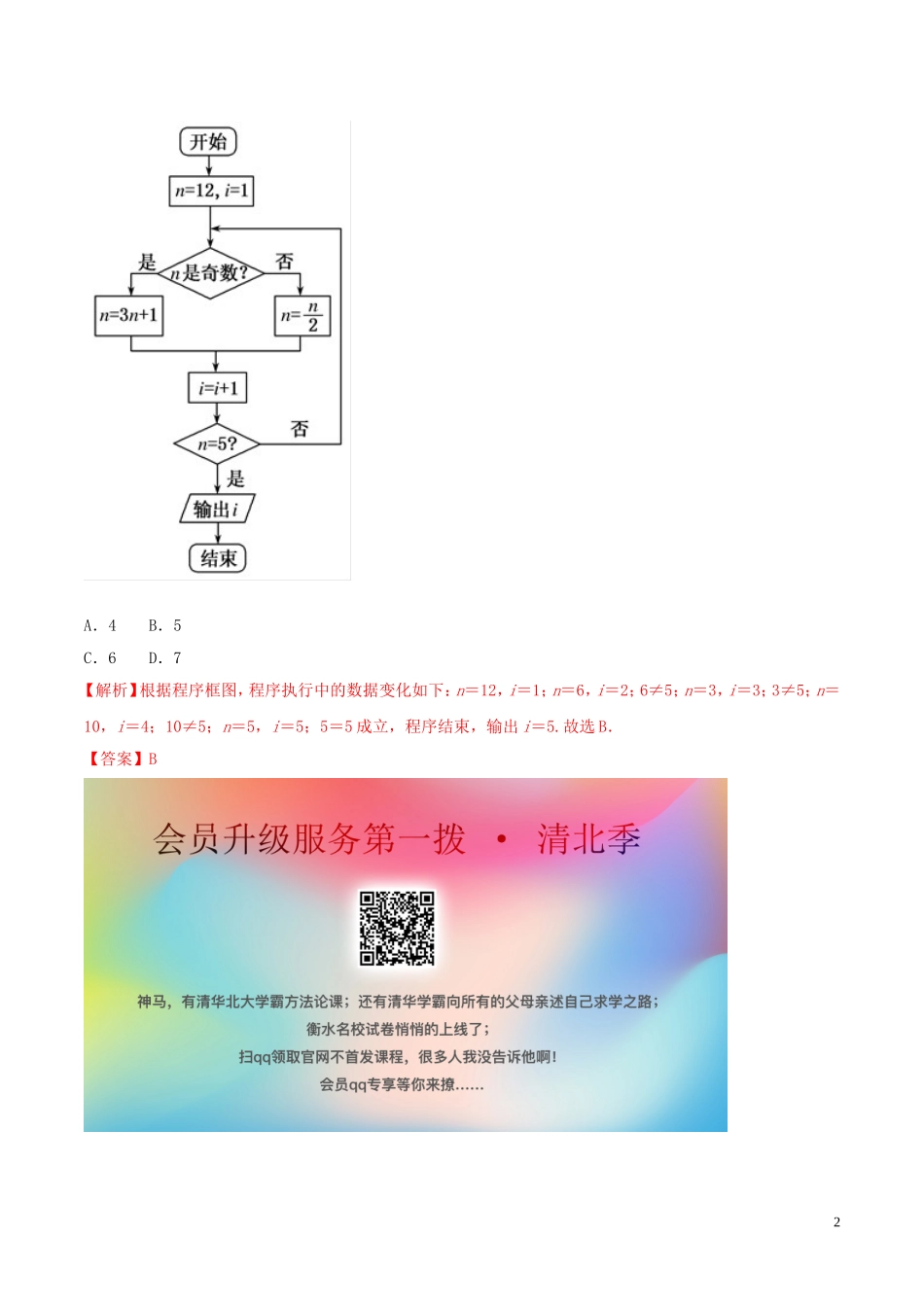
算法、复数【2019 年高考考纲解读】1.对于复数要掌握复数的概念、纯虚数、复数相等、复数的模、共轭复数等,以及复数的几何意义及四则运算(重点考查复数的乘除).2.对于程序框图要掌握基本算法语句尤其是含循环结构的程序框图,往往与分段函数的求值、数列求和或求积、统计等有规律的重复计算问题放在一起考查,读题审题要仔细.【重点、难点剖析】一、复数的概念与运算1.复数的乘法复数的乘法类似于多项式的四则运算,可将含有虚数单位 i 的看作一类项,不含 i 的看作另一类项,分别合并同类项即可. 【变式探究】执行如图所示的程序框图,运行相应的程序,若输出的结果是 4,则常数 a 的值为( )A.4 B.2 C. D.-1【解析】S 和 n 依次循环的结果如下:S=,n=2;S=1-,n=4.所以 1-=2,a=-1.故选 D.【答案】D【变式探究】若某程序框图如图所示,则该程序运行后输出的 i 的值为( )1A.4 B.5 C.6 D.7【解析】根据程序框图,程序执行中的数据变化如下:n=12,i=1;n=6,i=2;6≠5;n=3,i=3;3≠5;n=10,i=4;10≠5;n=5,i=5;5=5 成立,程序结束,输出 i=5.故选 B. 【答案】B2