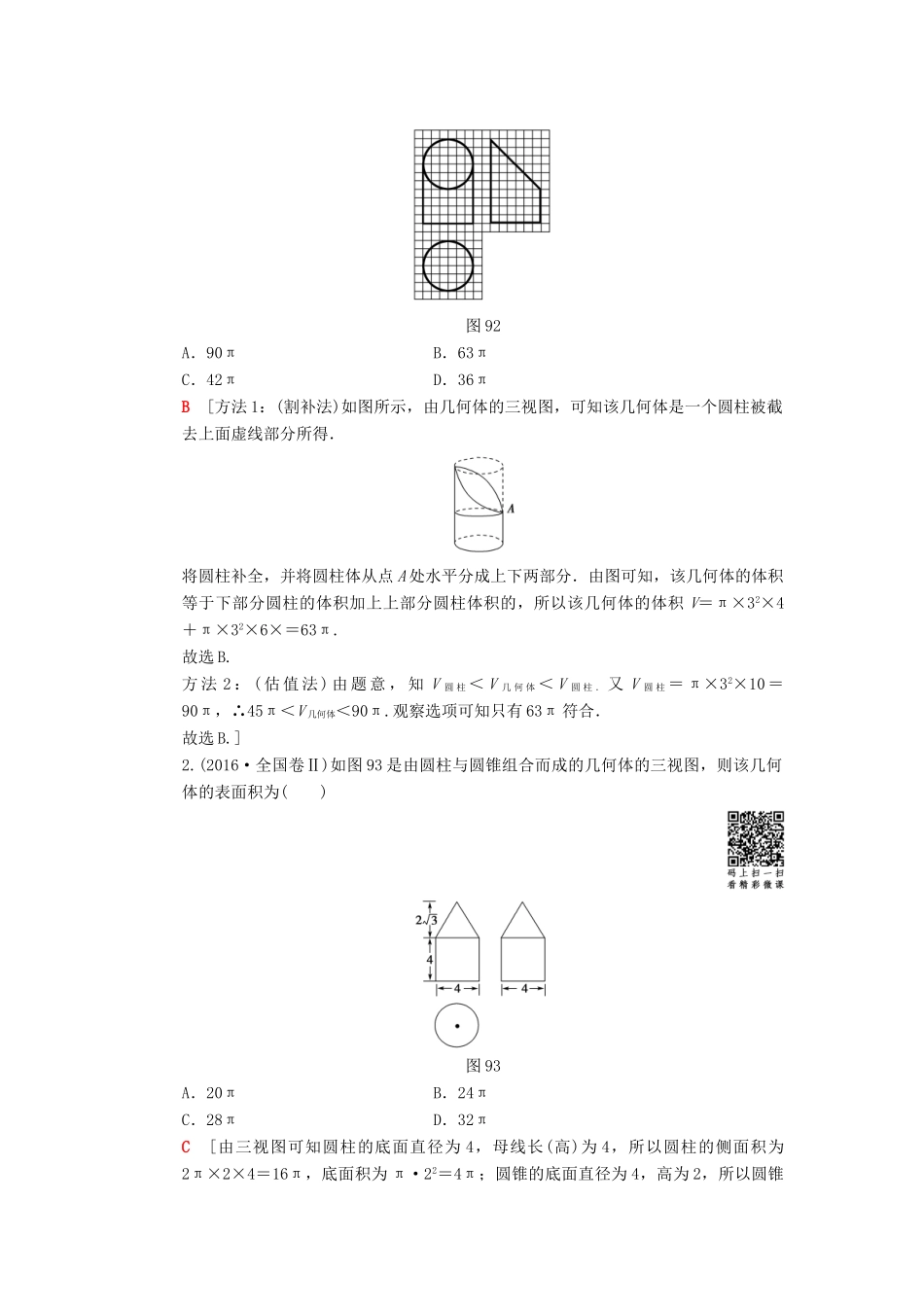
突破点 9 空间几何体表面积或体积的求解[核心知识提炼]提炼 1 求解几何体的表面积或体积(1)对于规则几何体,可直接利用公式计算.(2)对于不规则几何体,可采用割补法求解;对于某些三棱锥,有时可采用等体积转换法求解.(3)求解旋转体的表面积和体积时,注意圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形的应用.提炼 2 球与几何体的外接与内切(1)正四面体与球:设正四面体的棱长为 a ,由正四面体本身的对称性,可知其内切球和外接球的球心相同,则内切球的半径 r=a,外接球的半径 R=a.图 91(2)正方体与球:设正方体 ABCDA1B1C1D1的棱长为 a,O 为其对称中心,E,F,H,G 分别为 AD,BC,B1C1,A1D1的中点,J 为 HF 的中点,如图 91 所示.① 正方体的内切球:截面图为正方形 EFHG 的内切圆,故其内切球的半径为 OJ=;② 正方体的棱切球:截面图为正方形 EFHG 的外接圆,故其棱切球的半径为 OG=;③ 正方体的外接球:截面图为矩形 ACC1A1的外接圆,故其外接球的半径为 OA1=.[高考真题回访]回访 1 几何体的表面积或体积1.(2017·全国卷Ⅱ)如图 92,网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )图 92A.90π B.63πC.42π D.36πB [方法 1:(割补法)如图所示,由几何体的三视图,可知该几何体是一个圆柱被截去上面虚线部分所得.将圆柱补全,并将圆柱体从点 A 处水平分成上下两部分.由图可知,该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的,所以该几何体的体积 V=π×32×4+π×32×6×=63π.故选 B.方 法 2 : ( 估 值 法 ) 由 题 意 , 知 V 圆 柱 < V 几 何 体 < V 圆 柱 . 又 V 圆 柱 = π×32×10 =90π,∴45π<V 几何体<90π.观察选项可知只有 63π 符合.故选 B.]2.(2016·全国卷Ⅱ)如图 93 是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )图 93A.20π B.24πC.28π D.32πC [由三视图可知圆柱的底面直径为 4,母线长(高)为 4,所以圆柱的侧面积为2π×2×4=16π,底面积为 π·22=4π;圆锥的底面直径为 4,高为 2,所以圆锥的母线长为=4,所以圆锥的侧面积为 π×2×4=8π.所以该几何体的表面积为 S=16π+4π+8π=28π.]3.(2015·全国卷Ⅱ)一个正方体被...