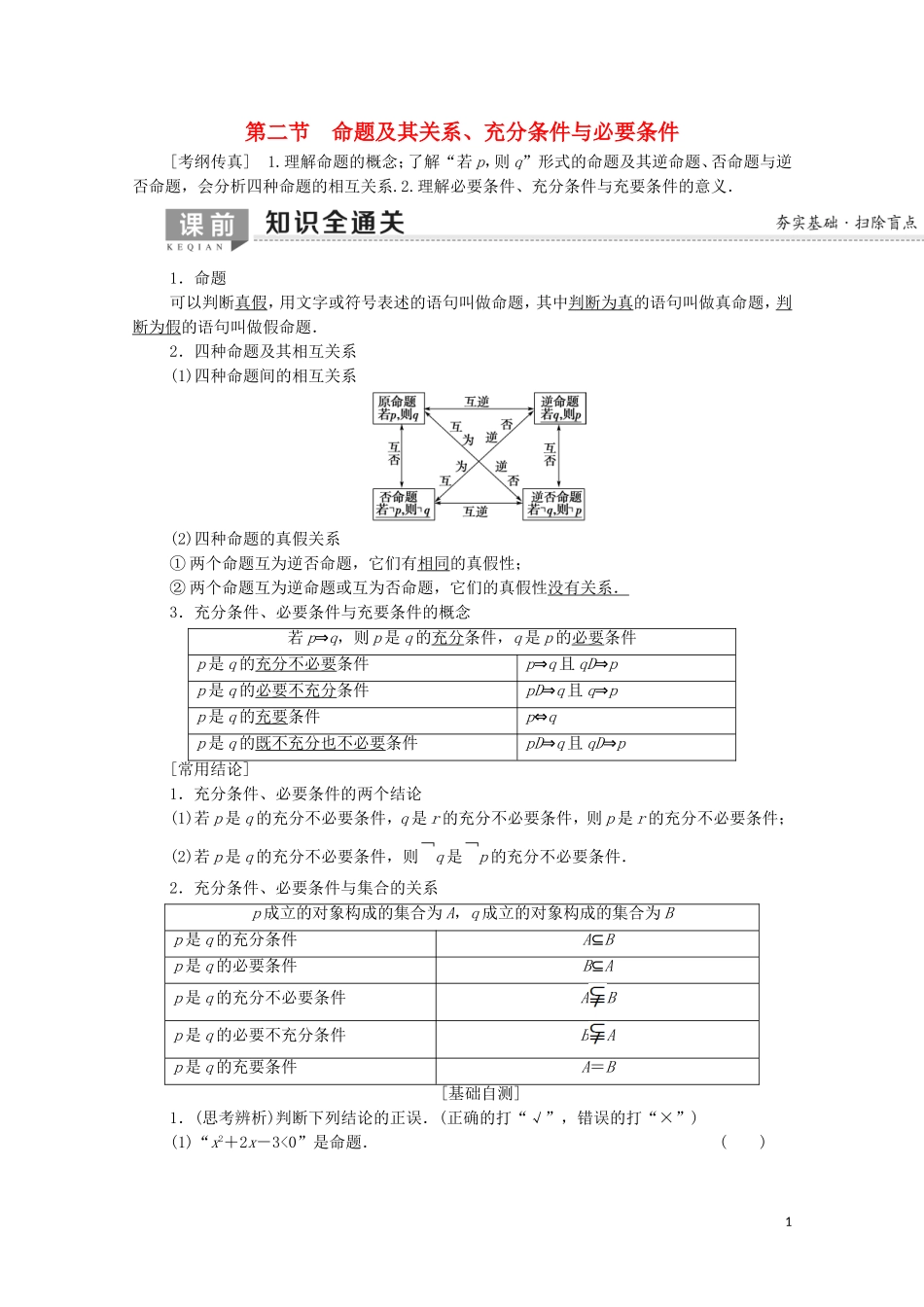
第二节 命题及其关系、充分条件与必要条件[考纲传真] 1.理解命题的概念;了解“若 p,则 q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.2.理解必要条件、充分条件与充要条件的意义.1.命题可以判断真假,用文字或符号表述的语句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.2.四种命题及其相互关系(1)四种命题间的相互关系(2)四种命题的真假关系① 两个命题互为逆否命题,它们有相同的真假性;② 两个命题互为逆命题或互为否命题,它们的真假性没有关系.3.充分条件、必要条件与充要条件的概念若 p⇒q,则 p 是 q 的充分条件,q 是 p 的必要条件p 是 q 的充分不必要条件p⇒q 且 qD⇒pp 是 q 的必要不充分条件pD⇒q 且 q⇒pp 是 q 的充要条件p⇔qp 是 q 的既不充分也不必要条件pD⇒q 且 qD⇒p[常用结论]1.充分条件、必要条件的两个结论(1)若 p 是 q 的充分不必要条件,q 是 r 的充分不必要条件,则 p 是 r 的充分不必要条件;(2)若 p 是 q 的充分不必要条件,则﹁q 是﹁p 的充分不必要条件.2.充分条件、必要条件与集合的关系p 成立的对象构成的集合为 A,q 成立的对象构成的集合为 Bp 是 q 的充分条件A⊆Bp 是 q 的必要条件B⊆Ap 是 q 的充分不必要条件ABp 是 q 的必要不充分条件BAp 是 q 的充要条件A=B[基础自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)“x2+2x-3<0”是命题.( )1(2)命题“若 p,则 q”的否命题是“若 p,则﹁q”.( )(3)当 q 是 p 的必要条件时,p 是 q 的充分条件.( )(4)“若 p 不成立,则 q 不成立”等价于“若 q 成立,则 p 成立”.( )[解析] (1)错误.该语句不能判断真假,故该说法是错误的.(2)错误.否命题既否定条件,又否定结论.(3)正确.q 是 p 的必要条件说明 p⇒q,所以 p 是 q 的充分条件.(4)正确.原命题与逆否命题是等价命题.[答案] (1)× (2)× (3)√ (4)√2.(教材改编)命题“若 α=,则 tan α=1”的逆否命题是( )A.若 α≠,则 tan α≠1B.若 α=,则 tan α≠1C.若 tan α≠1,则 α≠D.若 tan α≠1,则 α=C [“若 p,则 q”的逆否命题是“若﹁q,则﹁p”,显然﹁q:tan α≠1,﹁p:α≠,所以该命题的逆否命题是“若 tan α≠1,则 α≠”.]3.已知集合 A={1,...