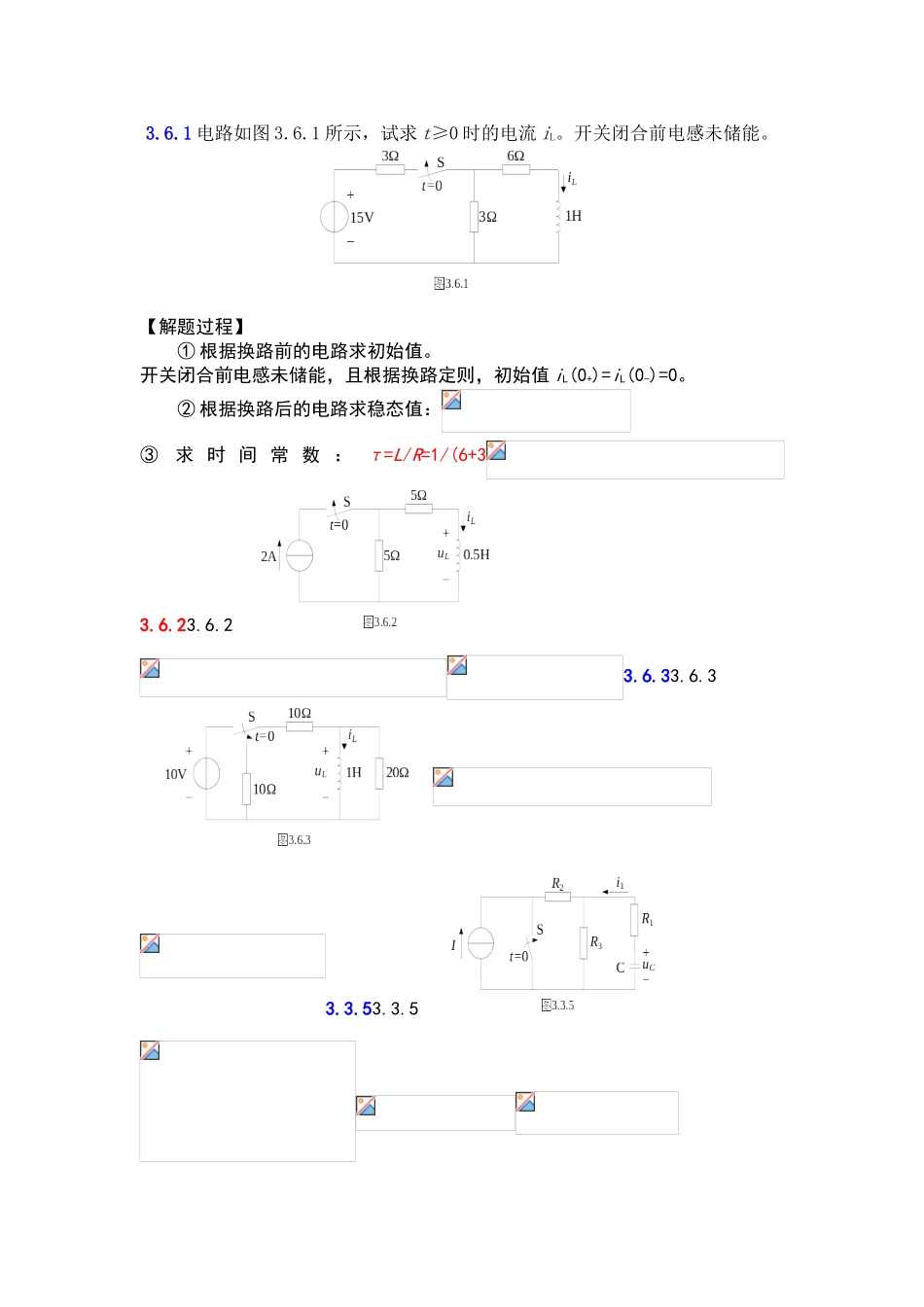
3.6.1 电路如图 3.6.1 所示,试求 t≥0 时的电流 iL。开关闭合前电感未储能。【解题过程】① 根据换路前的电路求初始值。开关闭合前电感未储能,且根据换路定则,初始值 iL(0+)=iL(0-)=0。② 根据换路后的电路求稳态值:③求 时 间 常 数 : τ=L/R=1/(6+33.6.23.6.23.6.33.6.33.3.53.3.53.3.63.3.63.4.13.4.13.4.23.4.23.4.33.4.33.4.43.4.4 容 电压 uC;(2).B 点电位 VB和 A 点电位 VA的变化规律。换路前电路处于稳态。【解题过程】用三要素法求解。① 求初始值,根据换路定则:uC(0+)=uC(0-)=[0-(-6)]×5/(5+25)=1V。然后根据换路后的电路,即 S 打开,并将电容看做电压为 uC(0+)的电压源,等效电路如上图所示。根据 KCL 可知流出和流出虚线圆圈的电流应该相等。[6-VB(0+)]/10=[VA(0+)-(-6)]/25,且 VB(0+)- VA(0+)=1V。求解可得:VB(0+)=,VA(0+)=。② 求稳态值。uC(∞)=[6-(-6)]×5/(10+5+25)= V;VB(∞)=6-[6-(-6)]×10/(10+5+25)=3V;VA(∞)=-6+[6-(-6)]×25/(10+5+25)=;③ 求时间常数。电容两端等效电阻为 Req=5×(10+25)/(5+10+25)=Ω,(为 5Ω 电阻与 10Ω即 25Ω 串联的并联),所以时间常数 τ=RC=4375×100×10-12=×10-7s。④ 将三要素代入公式得。;;。3.4.5 电路如图 3.4.5 所示,换路前已处于稳态,试求换路后(t≥0)的 uC。【解题过程】① 求初始值。根据换路前的电路,由换路定则 uC(0+)=uC(0-)=1×20-10=10V。注意:虽然求初始值时,电容所在支路无电流,但是要减去电压源的端电压。② 求稳态值。由换路后的电路,稳态值 uC(∞)= 20×1×10/(10+20+10)-10=−5V。③ 求时间常数。电 容 两 端 等 效 电 阻 为 Req=(10+10)//20=10kΩ , 所 以 时 间 常 数τ=RC=10×103×10×10-6=。④ 将三要素代入公式可得。。3.6.3在图3.6.3所示电路中U1=24V,U2=20V,R1=60Ω,R2=120Ω,R3=40Ω,L=4H。换路前电路已处于稳态,试求换路后的电流 iL。【解题过程】根据三要素法进行求解。① 由换路前的电路求初始值 iL(0+)。根据换路定则可知,iL(0+)=iL(0-)=U2/R3=20/40=。② 求稳态值。根据换路后的电路求稳态 iL(∞)。即 开 关 S 闭 合 , 电 感 认 为 短 路 , 所 以 电 阻 R2 被 短 路 , 所 以iL(∞)=U1/R1+U2/R3=24/60+20/40=。③ 求时间常数。将电源除零,电感两端等效电阻为 R=R1//R2//R3=20Ω,所以时间常数 τ=L/R=4/20=。...