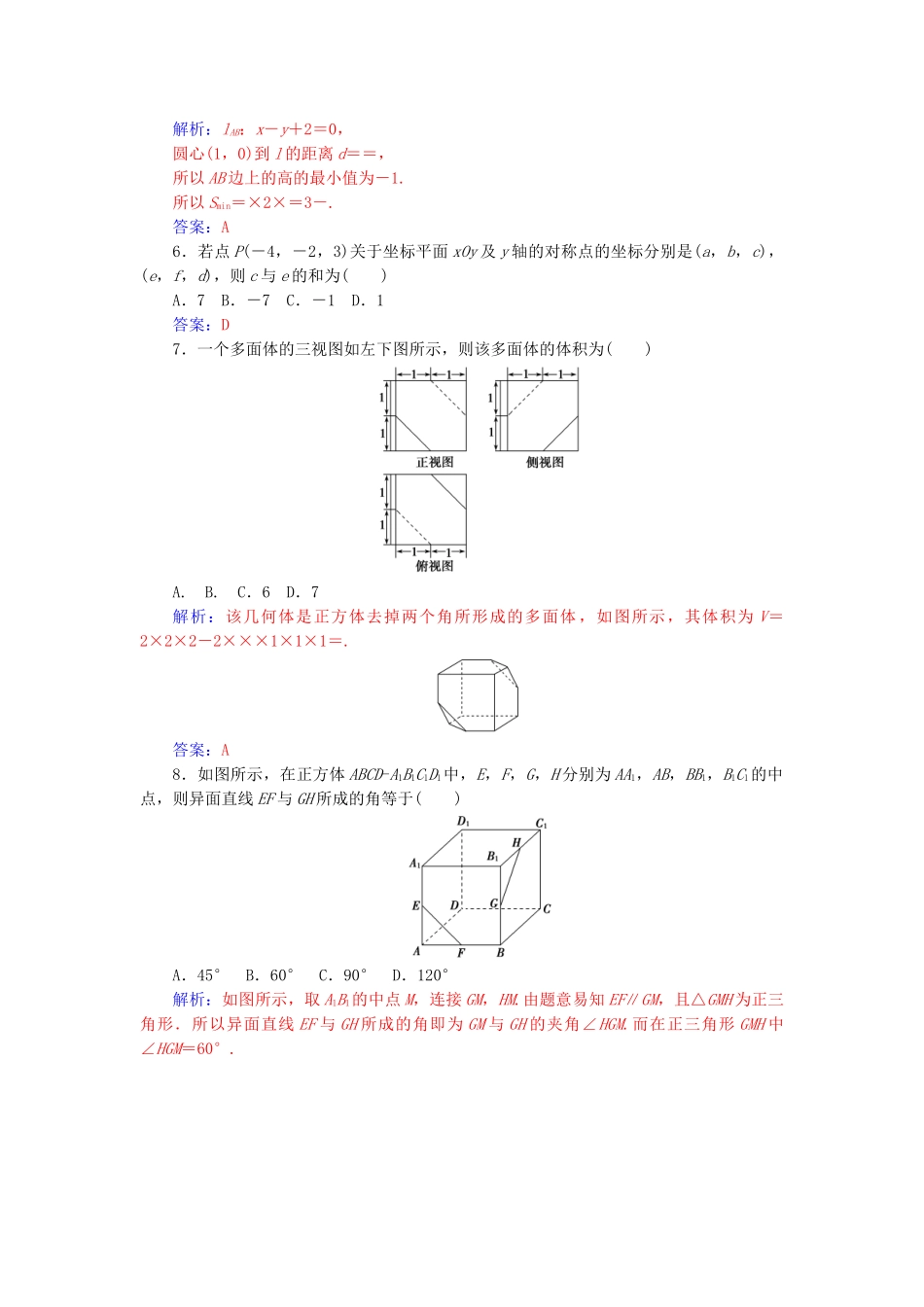
模块综合检测卷(二)(时间:120 分钟 满分:150 分)一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若 PQ 是圆 x2+y2=9 的弦,PQ 的中点是 M(1,2),则直线 PQ 的方程是( )A.x+2y-3=0 B.x+2y-5=0C.2x-y+4=0 D.2x-y=0解析:由题意知 kOM==2,所以 kPQ=-.所以直线 PQ 的方程为:y-2=-(x-1),即:x+2y-5=0.答案:B2.直线 l 通过两直线 7x+5y-24=0 和 x-y=0 的交点,且点(5,1)到 l 的距离为,则 l 的方程是( )A.3x+y+4=0 B.3x-y+4=0C.3x-y-4=0 D.x-3y-4=0解析:由得交点(2,2).设 l 的方程为 y-2=k(x-2),即 kx-y+2-2k=0,所以=,解得 k=3.所以 l 的方程为 3x-y-4=0.答案:C3.在坐标平面 xOy 上,到点 A(3,2,5),B(3,5,1)距离相等的点有( )A.1 个 B.2 个C.不存在 D.无数个解析:在坐标平面 xOy 内,设点 P(x,y,0),依题意得=,整理得 y=-,x∈R,所以符合条件的点有无数个.答案:D4.已知直线 l:x+ay-1=0(a∈R)是圆 C:x2+y2-4x-2y+1=0 的对称轴.过点A(-4,a)作圆 C 的一条切线,切点为 B,则|AB|=( )A.2 B.4 C.6 D.2解析:圆 C 的标准方程为(x-2)2+(y-1)2=4,圆心为 C(2,1),半径为 r=2,因此 2+a·1-1=0,a=-1,即 A(-4,-1),|AB|===6.答案:C5.已知两点 A(-2,0),B(0,2).点 C 是圆 x2+y2-2x=0 上任意一点,则△ABC 面积的最小值是( )A.3- B.3+C.3- D.解析:lAB:x-y+2=0,圆心(1,0)到 l 的距离 d==,所以 AB 边上的高的最小值为-1.所以 Smin=×2×=3-.答案:A6.若点 P(-4,-2,3)关于坐标平面 xOy 及 y 轴的对称点的坐标分别是(a,b,c),(e,f,d),则 c 与 e 的和为( )A.7 B.-7 C.-1 D.1答案:D7.一个多面体的三视图如左下图所示,则该多面体的体积为( )A. B. C.6 D.7解析:该几何体是正方体去掉两个角所形成的多面体 ,如图所示,其体积为 V=2×2×2-2×××1×1×1=.答案:A8.如图所示,在正方体 ABCD-A1B1C1D1中,E,F,G,H 分别为 AA1,AB,BB1,B1C1的中点,则异面直线 EF 与 GH 所成的角等于( )A.45° B.60° C.90° D.120°解析:如图所示,取 A1B1的中点 M,连接 GM,HM.由题...